Non, ça ne vas pas. Si
Vérification d'Intégrales
13 messages
- Page 1 sur 1
Salut,
Non, ça ne vas pas. Si\big)^n\,dx) alors
alors
\big)^0\,dx=\int_1^e1\,dx) qui est la surface d'un rectangle de largeur... et de hauteur...
qui est la surface d'un rectangle de largeur... et de hauteur...
\big)^1\,dx=\int_1^e\ln(x)\,dx) et il faut que tu trouve une primitive de x->ln(x) OU BIEN que tu fasse une intégration par partie OU BIEN un changement de variable...
et il faut que tu trouve une primitive de x->ln(x) OU BIEN que tu fasse une intégration par partie OU BIEN un changement de variable...
Non, ça ne vas pas. Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben... non :
Si tu parle de la première, je ne vois pas d'où sort le log népérien vu que la fonction à intégrer est x->1.
Si tu parle de la deuxième, je ne vois pas d'où sort la puissance 0 vu que la fonction à intégrer est x->ln(x).
Si tu parle de la première, je ne vois pas d'où sort le log népérien vu que la fonction à intégrer est x->1.
Si tu parle de la deuxième, je ne vois pas d'où sort la puissance 0 vu que la fonction à intégrer est x->ln(x).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Oui, mais une intégrale, cela représente l'aire sous la courbe, donc par exemple pour calculer l'intégrale  , je trouve que, plutôt que de chercher une primitive, il est plus simple de dire que I est la surface du rectangle de largeur 8-5=3 et de hauteur 2 donc que I=3x2=6.
, je trouve que, plutôt que de chercher une primitive, il est plus simple de dire que I est la surface du rectangle de largeur 8-5=3 et de hauteur 2 donc que I=3x2=6.
On peut encore utiliser cette méthode "visuelle" pour , qui correspond à la surface d'un trapèze (fait un dessin)
, qui correspond à la surface d'un trapèze (fait un dessin)
Pour revenir à ton problème, comme une primitive de x -> ln(x) est
x -> x ln(x)-x, on a effectivement :
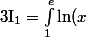\,dx=\Big[x\ln(x)-x\Big]_{x=1}^{x=e}\,=\big(e\ln(e)-e\big)\,-\,\big(1\ln(1)-1\big))
Mais je ne vois pas d'où peuvent bien sortir tes "exposants 0"...
On peut encore utiliser cette méthode "visuelle" pour
Pour revenir à ton problème, comme une primitive de x -> ln(x) est
x -> x ln(x)-x, on a effectivement :
Mais je ne vois pas d'où peuvent bien sortir tes "exposants 0"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
I0, c'est ça : \big)^0\,dx=\int_1^e1\,dx) .
.
Pense tu qu'une primitive de soit
soit -x\big)^0) ?
?
Personellement, je ne pense pas...
Je pense que tu est en train "d'inventer" une règle qui dirait que :
"si une primitive de f est F alors une primitive de f^n est F^n".
Je te rassure tout de suite, c'est totalement... faux :
une primitive de x->x est x->x²/2 et une primitive de x->x^n est
x->x^(n+1)/(n+1) qui n'est pas du tout égal à (x²/2)^n.
Pense tu qu'une primitive de
Personellement, je ne pense pas...
Je pense que tu est en train "d'inventer" une règle qui dirait que :
"si une primitive de f est F alors une primitive de f^n est F^n".
Je te rassure tout de suite, c'est totalement... faux :
une primitive de x->x est x->x²/2 et une primitive de x->x^n est
x->x^(n+1)/(n+1) qui n'est pas du tout égal à (x²/2)^n.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
