Vérification inéquation

par **Sophie74** » 31 Jan 2010, 23:02

Bonjour à tous!

5(1-lnx)(lnx-3)>1
(1-lnx)(lnx-3)>1/5
lnx-3-ln^2(x)+3lnx>1/5
2lnx>-14/5
lnx>-7/5
x>e^(-7/5)

Quelqu'un pourrait me dire si c'est juste? Si c'est faux, merci de corriger!

par **Sophie74** » 31 Jan 2010, 23:25

5(1-lnx)(lnx-3)>1
(1-lnx)(lnx-3)>1/5
lnx-3-ln^2(x)+3lnx>1/5
2lnx>16/5
lnx>8/5
x>e^(8/5)

Ca serait pas plutôt ça?

par **Finrod** » 31 Jan 2010, 23:39

Entre la ligne 3 et 4.. comment tu passe d'un polynôme du second degrès en ln(x) plus grand qu'un truc à une inégalité juste sur ln(x) ?

J'intuite que tu as fait

, donc problème, car le carré est en dehors.

Je pense qu'il faut étudier le polynôme du second degrès en posant X=ln(x)

puis une fois que tu as les inégalité pour X, passer au exponentielles

(vu l'heure, bon courage)

par **Sophie74** » 31 Jan 2010, 23:42

oulah... ça m'a l'air vraiment compliqué :cry:

par **Finrod** » 31 Jan 2010, 23:46

Il faut juste trouver les X tels que -X²+4X-16/5>0 . si y et z sont les solutions, yz et hop tu passes à l'exponentielle directement.

par **Sophie74** » 31 Jan 2010, 23:47

Peux tu m'aider?

par **Finrod** » 31 Jan 2010, 23:52

Je pense que tu peux trouver les deux solutions avec le delta, ça, ça va.

Après tu dois avoir dans ton cours que le signe du polynôme est l'opposé du signe du coeff devant le X² entre les deux solutions de P(X)=0, notées ici y et z.

Donc c'est l'inverse de ce que j'ai dit dans mon post précédant, y<X<z.

je ne donne pas les valeurs exactes de y et z car comme elles n'ont pas l'air de se simplifier, je voie pas trop l'interêt. Mais je suppose que toi tu dois le faire.

donc

comme l'exponentielle est croissante.

par **Sophie74** » 01 Fév 2010, 12:56

:doh: et ça donne quoi?

par **Finrod** » 01 Fév 2010, 13:09

t'as réussi à trouver y et z ? il n'y a rien de plus.

par **Sophie74** » 01 Fév 2010, 13:11

non je n'ai pas trouvé :triste:

par **Finrod** » 01 Fév 2010, 13:16

il faut résoudre -X²+4X-16/5 = 0

Le discriminant

est égal à b²-4ac, ici b=4, c=-16/5 et a=-1 donc il vaut : ....

Les solutions sont de la forme

elles valents donc ...

Le polynôme sera positif entre les deux racines.

Je te laisse compléter. Ton cours contient certainement des indications aussi précises que celles-ci.

par **Sophie74** » 01 Fév 2010, 13:29

-X²+4X-16/5 = 0
b²-4ac=-4²-4*-1*-16/5
=-80

-b+rac(delta)/2=4+rac(80)/2=6.47
-b-rac(delta)/2=4-rac(80)/2=-2.47
c'est juste?

par **Ben314** » 01 Fév 2010, 13:49

Ben....
Pas vraiment, pour b²-4ac tu devrait trouver ?/5 ...

par **Sophie74** » 01 Fév 2010, 14:51

je vois pas ce que j'ai fais de faux... :cry:

par **Ericovitchi** » 01 Fév 2010, 16:08

pratiquement tout
b²-4ac=(-4)²-4*(-1)*(-16/5)=16-4*16/5=(5*16-4*16)/5=16/5
pas grand chose à voir avec - 80

Bref tes racines valent

et

Essayes de finir l'exercice

(Tu dois trouver

mais disons que je ne t'ai rien dit)

par **Sophie74** » 01 Fév 2010, 17:40

et il faut faire comment pour arriver à ce résultat à partir des racines? (je n'ai jamais vu cette règle...)

par **Finrod** » 01 Fév 2010, 17:43

Ericovitchi à utiliser le fait que

qui vient du fait que

par **Sophie74** » 01 Fév 2010, 17:54

oui, mais je n'ai jamais vu cette règle :doh:
Je vois pas comment on termine l'inéquation...

par **Finrod** » 01 Fév 2010, 18:15

Si tu est parfaitement capable de calculer x/x² = 1/x avec x =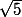

ça n'a rien d'une "règle", c'est un calcul que tu as sans doute déjà fait. Ca fait un peu bizarre avec une racine, mais on s'habitue vite.

vu les résultats que t'as donné Ericovitchi, il ne te reste plus que des somme, soustractions, quotients et multiplications avec des fractions et des racines. Tu peux y arriver.

par **Sophie74** » 01 Fév 2010, 19:50

5(1-lnx)(lnx-3)>1
(1-lnx)(lnx-3)>1/5
lnx-3-ln^2(x)+3lnx>1/5

delta= b²-4ac= (-4)²-4*(-1)*(-16/5)=16-4*16/5=(5*16-4*16)/5=16/5

racine: -b+-rac(delta)/2
x1= 4+rac(16/5)/2=2.89
x2= 4-rac(16/5)/2=1.11

je trouve ça comme racine... J'ai pas fais une erreur?

Vérification inéquation

vérification inéquation

Qui est en ligne