Vecteurs et parallélograme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 24 Mai 2009, 14:15
par titine » 24 Mai 2009, 14:15
Grégoire35 a écrit:Bonjour a tous , je suis sur un exercice et je bloque sur certaines question , voilà l'énoncé :
a) dans un repère orthonormal ,tracer les droites 1 et 2 d'équations respectives :y=x+1 et y=-2x+7
b) justifier le fait que les 2 droites sont sécantes , lire les coordonnées de leur point d'intersection noté A , faire un vérification par le calcul .
c) 1 coupe l'axe des ordonnées en d et 2 coupe l'axe des ordonnées en B
Quelles sont les coordonnées de D et B ?
d) trouver les coordonnées de de C tel que ABCD soit un parallélograme , calculer l'aire de ABCD .
c'est le début de la question b et la question d qui me dérangent , vos conseils sont les bienvenus .
La première a pour coefficient directeur 1, la deuxième a pour coefficient directeur -2. Donc elles ne sont pas parallèles. Donc elles sont sécantes !
Pour que ABCD soit un parallélogramme il faut que vec(AB) = vec(DC)
Ecris les coordonnées de ces 2 vecteurs ....

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 14:33
par Ericovitchi » 24 Mai 2009, 14:33
si le point est à la fois sur les deux droites y=x+1 et y=-2x+7 c'est que ses coordonnées x,y satisfont les deux équations donc le voilà ton système d'équations. Il te suffit d'ailleurs d'égaler les deux valeurs de y et de trouver x

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 14:55
par Ericovitchi » 24 Mai 2009, 14:55
Oui (et 6/3 = 2 accessoirement)
Tu remplaces dans l'une ou l'autre pour trouver le y car évidemment tu vas trouver la même valeur

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 15:41
par Ericovitchi » 24 Mai 2009, 15:41
tu écris par exemple que
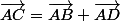
tu sais calculer le membre de droite donc tu vas en déduire les coordonnées de C

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 18:15
par Ericovitchi » 24 Mai 2009, 18:15

théorème de chasles
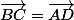
parce que l'on est dans un parallélogramme
donc
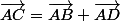
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
