Vecteurs mathématique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:09
par azertyqsdfg » 11 Oct 2014, 23:09
mathelot a écrit:oui.
Après il s'agit de vérifier que leurs coordonnées sont proportionnelles.
Il faut aboutir à une équation du second degré (un trinome).
Peux tu me la donner? Me l'expliquer? (Car il me semble que je ne l'ai pas fait en cours ça (aboutir à une équation pour verifier)) :mur:
-
mathelot
 par mathelot » 11 Oct 2014, 23:14
par mathelot » 11 Oct 2014, 23:14
azertyqsdfg a écrit:Bonjour, voilà un énoncé :
Pour quelles valeurs de "t" les points A(3;2), B(1;t) et C(t;1) sont-ils alignés ?
)
)
après, on essaye d'écrire que
-2

t-2
t-3

-1
forment un tableau de proportionnalité.
Comment procéderais tu ?
-
mathelot
 par mathelot » 11 Oct 2014, 23:20
par mathelot » 11 Oct 2014, 23:20
:dodo: .............................
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:25
par azertyqsdfg » 11 Oct 2014, 23:25
mathelot a écrit:dépêches, svp.
tu as une égalité de quotients à écrire(ça marche comme pour les fractions)
5,4,3,2,1,0 trop tard, je suis tombé dans les bras de Morphée (la déesse du sommeil) :dodo:
pas besoin de tableau. Juste dit moi le calcul qui justifie que t=1 ! Car moi je l'ai trouvé de tête car c'était pas compliquer mais comment prouver? :dodo:
-
mathelot
 par mathelot » 11 Oct 2014, 23:28
par mathelot » 11 Oct 2014, 23:28
je te fais passer par le tableau de proportionnalité car c'est programme de Cinquième-4ème.
c'est sensé faciliter la compréhension.
On est encore loin du résultat car on doit trouver une équation du second degré. :hum:
-
mathelot
 par mathelot » 11 Oct 2014, 23:30
par mathelot » 11 Oct 2014, 23:30
azertyqsdfg a écrit:pas besoin de tableau. Juste dit moi le calcul qui justifie que t=1 ! Car moi je l'ai trouvé de tête car c'était pas compliquer mais comment prouver? :dodo:
oui,oui.
mais il y a une autre valeur possible.
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:30
par azertyqsdfg » 11 Oct 2014, 23:30
mathelot a écrit:oui,oui.
mais il y a une autre valeur possible.
J'en peux plus .... :mur: :mur:
-
mathelot
 par mathelot » 11 Oct 2014, 23:34
par mathelot » 11 Oct 2014, 23:34
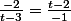
par l'égalité des produit en croix:
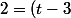(t-2))
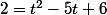
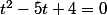
On vérifie que t=1, mais également t=4, sont solutions.
on admettra qu'une équation du second degré n'a pas plus de deux solutions.
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:38
par azertyqsdfg » 11 Oct 2014, 23:38
mathelot a écrit: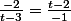
par produit en croix
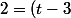(t-2))
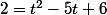
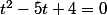
On vérifie que t=1, mais également t=4, sont solutions.
on admettra qu'une équation du second degré n'a pas plus de deux solutions.
Je dois avouer que .... j'ai pas réfléchis .... il est peut être un peu trop tard
Merci quand même. A+
-
mathelot
 par mathelot » 11 Oct 2014, 23:40
par mathelot » 11 Oct 2014, 23:40
si c'est un exercice donné en Seconde, c'est bien "difficile".
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:44
par azertyqsdfg » 11 Oct 2014, 23:44
mathelot a écrit:si c'est un exercice donné en Seconde, c'est bien "difficile".
Quoi ....... je crois que je me suis trompé de catégorie? Je suis en 1ere S....
Bref bonne nui a tous, merci pour votre aide. :zen:
-
mathelot
 par mathelot » 11 Oct 2014, 23:46
par mathelot » 11 Oct 2014, 23:46
quand tu dis , au début de la conversation,
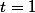
, j'aurai dû acquiescer,
parce que c'était juste,
on peut effectivement trouver des solutions évidentes.
Peut être , ensuite, il y avait une méthode pour trouver l'autre valeur
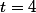
sans passer
par un trinome.
désolé.
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:48
par azertyqsdfg » 11 Oct 2014, 23:48
mathelot a écrit:quand tu dis , au début de la conversation,
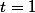
, j'aurai dû acquiescer,
parce que c'était juste,
on peut effectivement trouver des solutions évidentes.
Peut être , ensuite, il y avait une méthode pour trouver l'autre valeur
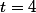
sans passer
par un trinome.
désolé.
Oui je pense aussi mais je vais marquer ton calcul.
Mais comment ça par produit en croix ? J'ai pas compris juste ça
-
mathelot
 par mathelot » 11 Oct 2014, 23:51
par mathelot » 11 Oct 2014, 23:51
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 11 Oct 2014, 23:58
par azertyqsdfg » 11 Oct 2014, 23:58
mathelot a écrit: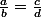
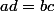
merci a toi. A+
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 12 Oct 2014, 09:46
par paquito » 12 Oct 2014, 09:46
Tu pouvais éviter de passer par le critère de colinéarité (Produit en croix nuls), même si c'est à connaître en écrivant
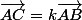
, ce qui te donnait:
(1) t-3=-2k et
(2) -1=(t-2)k;
(1) te donne
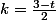
et en reportant dans (2), on obtient -2=(t-2)(3-t) ce qui te redonnes:
t^2-5t+4=0, équation du second degré qu'il est impératif de savoir résoudre en 1°S , de même le fait qu'une équation du second de gré admette au plus 2 racines est un résultat qui a été démontré dans le cadre du cours sur le 2° degré! A mon avis, il est temps que tu te réveilles!
-
azertyqsdfg
- Membre Naturel
- Messages: 28
- Enregistré le: 13 Sep 2014, 12:16
-
 par azertyqsdfg » 12 Oct 2014, 11:23
par azertyqsdfg » 12 Oct 2014, 11:23
paquito a écrit:Tu pouvais éviter de passer par le critère de colinéarité (Produit en croix nuls), même si c'est à connaître en écrivant
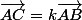
, ce qui te donnait:
(1) t-3=-2k et
(2) -1=(t-2)k;
(1) te donne
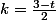
et en reportant dans (2), on obtient -2=(t-2)(3-t) ce qui te redonnes:
t^2-5t+4=0, équation du second degré qu'il est impératif de savoir résoudre en 1°S , de même le fait qu'une équation du second de gré admette au plus 2 racines est un résultat qui a été démontré dans le cadre du cours sur le 2° degré! A mon avis, il est temps que tu te réveilles!
Je sais résoudre une équation du second degré merci ... --'
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 12 Oct 2014, 13:31
par paquito » 12 Oct 2014, 13:31
azertyqsdfg a écrit:Je sais résoudre une équation du second degré merci ... --'
J'en suis convaincu, mais tu savoir qu'il y a 0, 1 ou 2 racines; il n'y as pas d'autres cas; c'est parce que tu as dit: admettons qu'une équation du second degré n'admette pas plus de 2 solutions que j'ai un peu tiqué; n'en parlons plus et bon dimanche.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
