Vecteurs mathématique

[azertyqsdfg]

Bonjour, voilà un énoncé :
Pour quelles valeurs de "t" les points A(3;2), B(1;t) et C(t;1) sont-ils alignés ?

Comment faire ? :mur: :mur:
Merci d'avance. :help:

[mathelot]

bonsoir,

écrire par exemple des tableaux de proportionnalité entre les
coordonnées des vecteurs

(il faut passer de l'affine(=points) au vectoriel (=vecteurs) avant de mettre en oeuvre la proportionnalité)

[azertyqsdfg]

À vrai dire, comment faire? Je ne comprends pas votre méthode...

[titine]

Bonjour, voilà un énoncé :
Pour quelles valeurs de "t" les points A(3;2), B(1;t) et C(t;1) sont-ils alignés ?

Comment faire ? :mur: :mur:
Merci d'avance. :help:

Les points A , B et C sont alignés si les vecteurs vec(AB) et vec(AC) sont colinéaires.
vec(AB) (1-3 ; t-2)
vec(AC) (t-3 ; 1-2)
Ces 2 vecteurs sont colinéaires si ...............
Tu en déduis t.

[mathelot]

i) tableau de proportionnalité (4ème)


1 2 3
5 10 15

les vecteurs u(1;2) et v(5;10) sont colinéaires car leurs coordonnées sont proportionnelles


c'est valable aussi en vecteurs colonnes.

ii)

sinon écrire determinant(u;v)=0, mais ce n'est pas au programme.

grillé par Titine :we:

[azertyqsdfg]

Ce sont des moins ou des tirets que vous avez mis ?

[mathelot]

ce sont des moins, elle passe d'affine au vectoriel



A,B: points, éléments d'un espace affine comme une droite, un plan

droite vectorielle: ensemble de vecteurs , portés par une direction de droite
tous colinéaires entre eux.

[azertyqsdfg]

i) tableau de proportionnalité (4ème)


1 2 3
5 10 15

les vecteurs u(1;2) et v(5;10) sont colinéaires car leurs coordonnées sont proportionnelles


c'est valable aussi en vecteurs colonnes.

ii)

sinon écrire determinant(u;v)=0, mais ce n'est pas au programme.

grillé par Titine :we:

T est donc égal à 1 ?

[azertyqsdfg]

Donc : xb - xa ; yb - ya doit être égal à xc - xa ; yc - ya ?? :cry:

[mathelot]

oui, mais encore ?

[azertyqsdfg]

oui, mais encore ?

mais encore quoi ? (Désolé mais j'ai un peu du mal) :mur:

[mathelot]

imaginons deux vecteurs colinéaires:



dans n'importe quelle base (=éléments vecteurs du repère)





on déduit de la colinéarité



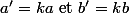
et



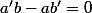
la réciproque est vraie.

si


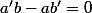
supposons





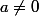
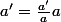
est le coeff de proportionnalité

il y a proportionnalité entre les coordonnées des vecteurs

conclusion: écrire

[azertyqsdfg]

imaginons deux vecteurs colinéaires:



dans n'importe quelle base (=éléments vecteurs du repère)





on déduit de la colinéarité



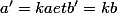
et



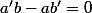
la réciproque est vraie.

si
a'b-ab'=0

supposons

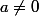
b'=\frac{a'}{a} b
a'= \frac{a'}{a} a



il y a proportionnalité entre les coordonnées des vecteurs

conclusion: écrire

C'est bon je viens de comprendre (titine aussi je viens de comprendre ce qu'elle disait)

[azertyqsdfg]

C'est bon je viens de comprendre (titine aussi je viens de comprendre ce qu'elle disait)

t est donc égal à 1 ?

[mathelot]

extra. cependant, nous trouvons une équation du second degré avec deux valeurs pour t.

[azertyqsdfg]

C'est bon je viens de comprendre (titine aussi je viens de comprendre ce qu'elle disait)

Donc: V=(-2;1)
U=(-2;1)

xy' - x'y = 0
-2×(-1) - (-1)×(-2) =0
2 - 2 =0

Donc colinéaires ? It's ok?

[mathelot]

Il s'agit d'écrire d'abord les coordonnées des deux vecteurs (no,itsn't)

AB et AC

qu'on écrit avec flèches

et

avec trois points, on passe d'abord en vectoriel.

[azertyqsdfg]

Je remplace V par AB
Et U par AC c'est tout?

[azertyqsdfg]

Il s'agit d'écrire d'abord les coordonnées des deux vecteurs (no,it'snt)

AB et AC

qu'on écrit avec flèches

et

avec trois points, on passe d'abord en vectoriel.

Donc je réécris :

AB=(-2;1)
AC=(-2;1)

xy' - x'y = 0*
-2×(-1) - (-1)×(-2) =0
2 - 2 =0

Donc colinéaires ?

[mathelot]

Je remplace V par AB
Et U par AC c'est tout?

oui.

Après il s'agit de vérifier que leurs coordonnées sont proportionnelles.

Il faut aboutir à une équation du second degré (un trinome).