Vecteur

[Partouche]

Soit ABC un triangle non aplati, A', B' et C' les milieux respectifs des segments [BC], [AC] et [AB] et O le centre du cercle circonscrit au triangle ABC.
SOit H le point défini par : OH= OA + OB + OC ( ceci est des vecteur)

1): déterminer le point H
a) MOntrer successivement que
AH=2OA' ; BH= 2OB' ; CH=2OC'

c) MOntrer successivement que :
(AH)perpendiculaire(BC)
(BH)perpendiculaire(AC)
(CH)perpendiculaire(AB)

Voila je bloque dés le début pour résoudre le calcul H !

[armor92]

Bonsoir partouche,

1) a)
Je ne comprend paas très bien ce que l'énoncé veut dire par "déterminer le point H"
Sinon on peut démontrer les relations
par SCHALES
= +
= + + +
= +

A' milieu de BC donc : + = 2

D'ou finalement : = 2

La démonstration est similaire pour les deux autres relations

[armor92]

1) c)

O le centre du cercle circonscrit est l'intersection des médiatrices de chacun des trois cotés.
OA' est donc sur la médiatrice du segment [BC], par définition OA' est perpendiculaire à BC.
Comme on démontré que les deux vecteurs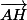 et 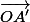sont colinéaires, nous avons AH // OA'

AH // OA' perpendiculaire BC, donc AH perpendiculaire OA'

La démonstration est similaire pour (BH)perpendiculaire(AC) et (CH)perpendiculaire(AB)

[Partouche]

Merci pour tout, j'ai réussi a faire la suite mais j'ai une questions !
POurquoi quand AH= AO + OH sa devient AO + OA + OB + OC ??

Enfin apres avoir résolu des question, je retombe encore dans des questions que j'arrive pas
3b ) GA + GB + GC = 0 ( vecteur nul )
MOntrer ensuite que AG= 2/3 AA'

3c) MOntrer que, pour tout point M du plan :
MA + MB + MC = 3MG

En déduire que OH= 3OG

VOila, ce sont les dernieres question auxquels je bloque :hum:

[armor92]

Merci pour tout, j'ai réussi a faire la suite mais j'ai une questions !
POurquoi quand AH= AO + OH sa devient AO + OA + OB + OC ??

C'est dans l'énoncé, H est défini par :
= +

3b) + + =
C'est la définition de G est centre de gravité du triangle ABC

On transforme la relation :
= +

On fait intervenir le milieu A' du segment [BC] (relation de schales)
= + + +

A' est milieu de [BC] donc + =

IL reste : = 2
On utilise la relation de schales :
= 2 ( + )
Ce qui donne :
3 = 2

[armor92]

3) c)
C'est une propriété du barycentre. pour le démontrer on utilise la relation de schales (encore une fois !)
+ + = + + + + +
= 3
(car + + = )

En particulier on peut prendre M = O
On a alors :
+ + = 3
Mais par hypothèse :
+ + =

C'est la relation cherchée