Bonjour je rame depuis plusieurs jour impossible de trouver même de décoller de la consigne, j'aimerai vraiment que quelqu'un m'aide .. même par Message privé, msn si ça lui convient mieux ..
EXERCICE 1 : Soit

;
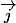)
une base du plan. On pose
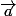
=

+
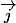
et
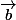
=

-
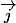
. Tracer (

;
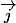
),
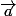
et
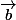
sur une feuille quadrillé
1. Déterminer les coordonnées de
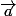
et
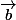
dans la base (

)
2. Montrer, en raisonnant par l'absurde, que
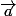
est différent de

et
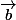
différent de
 3.
3. Montrer, en raisonnant par l'absurde, que
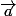
et
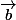
ne sont pas colinéaires. Que peut-on en déduire pour (

) ?
4. Tracer le vecteur
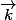
de coordonnées (-2;-1) dans la base (

)
5. Déterminer les coordonnées du vecteur
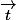
= 2
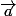
-
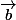
dans la base (

)
6. Déterminer les coordonnées du vecteur
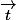
=
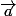
- 3
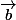
dans la base (

)
7. Calculer
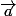
+
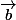
. En déduire l'expression de

dans la base (

)
8. Déterminer l'expression de
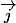
dans la base (

)
9. Déterminer les coordonnées du vecteur

=

- 2
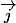
dans la base (

)
Voila je me suis investie pour faire un truc présentable jespère être aidé.. Merci d'avance

