Vecteur notmal d'un plan

[Khalantos]

Bonsoir à tous/toutes,

J'aimerais savoir comment je fait pour trouver un vecteur normal de plan avec les équations suivantes...

voici les informations que je dispose:

Soit le plan II

x=2+3r+-5s
y=-1+2r+s
z=3-2r-7s

où r,s E R


Je cé que dans ceci j'ai un point,apllelon le P(2,-1,3) et deux vecteurs directeurs D1(3,2,-2) et D2(5,1,-7).

Merci pour vôtre aide!

[XENSECP]

2 vecteurs directeurs qui sont orthogonaux au vecteur normal... donc ...? :)

[Anonyme]

@Khalantos

Il y a 2 méthodes :

1)
le produit vectoriel ( qui à priori n'est pas connu au lycée)

Si 2 vecteurs directeurs du plan sont de coordonnées (3,2,-2) et de coordonnées (5,1,-7)

alors ^ 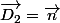est un vecteur normal du plan

2)
L'équation cartésienne du plan : Comme on est dans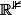
le plan a une équation cartésienne du type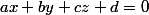 avec

et le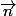 de coordonnées (a,b,c) est un vecteur normal du plan

[Khalantos]

Est-ce que je trouve l'équation ax+by+cz+d=0 ey je prend le vecteur N(a,b,c),ou ya moyen avec produit vectoriel ou autre?

formule R(un point) P(un point quelquonque) et N(a,b,c)

N*RP=0

[Khalantos]

AH merci ptitnoir...mon prof nous a fait acheté un livre qui date de 2003 et les explications ne sont pas très clair et il n'y a que des exercices ou presque...Et quelque définitions...Je suis du québec et moi c'est le collège mais sa doit être lycée pour vous en france.

Merci encore à vous deux!

[Khalantos]

alors le vecteur normal serais N(15,2,14)?

[Anonyme]

alors le vecteur normal serais N(15,2,14)?

Tu peux vérifier toi même en calculant et
car tu dois trouver 0

ps)
on travaille dans muni d'une repère orthonormé de donc muni d'un d'un produit scalaire

[Khalantos]

merci beaucoup pour ce truc,sa donne vriament 0.

sa fait 2-3 jours que je me casse la tête la dessus et ya personne qui pouvais m'aider dans ma famille amis.

[Anonyme]

@Khalantos
Et bien maintenant tu sais qu'il y a éventuellement Maths-Forum qui peut te venir en aide
Bonne fin de we

[Anonyme]

P(2,-1,3) et deux vecteurs directeurs D1(3,2,-2) et D2(5,1,-7)

@Khalantos

Autre explication :
L'équation cartésienne du plan : avec

se trouve en disant qu'un point M de coordonnées (x,y,z) appartient au plan
si et seulement si le système ( ) est lié ( non libre )
en calculant le déterminant de ce système qui est égal à 0

[Khalantos]

J'ai un autre petit soucis, avec une équation symétrique d'une droite...

-x+3/2=y/3=z-1/5

avant d'utilisé le vecteur directeur de la droite D(2,3,5)

est-ce que je doit rendre mon x positif comme cela

x-3/-2=y/3=z-1/5

[Anonyme]

@Khalantos
Peux tu expliquer ce qu'est une équation symétrique d'une droite car je ne connais pas cette notion

Ce que j'ai compris de ton exo : c'est qu'il y a 2 équations
-x+3/2=y/3
et
y/3=z-1/5

ce qui donne un système 3 équations paramétrées ( j'ai pris y comme paramètre )
x = 3/2 - y/3
y = y
z = 1/5 +y/3

Qui représente une droite dont un des vecteurs directeurs a pour coordonnées ( -1/3 , 1 , 1/3 )


ps)
Un autre vecteur directeur de cette droite a pour coordonnées ( 1 , -3 , -1)
avec un x positif comme "évoqué" dans ton message...

[Anonyme]

@Khalantos

Essaie la prochaine fois d'éviter de créer 2 discussions différentes sur le même sujet
car cela ne sert à rien

Il vaut mieux avoir toutes les explications sous une même et unique discussion
A+

Je fais référence à:
http://www.maths-forum.com/verifier-parallele-plan-r3-133090.php