Vecteur directeur droite au croisement de deux plans

[Kugge]

Bonjour
Lorsqu'une droite est défini par l'équation cartésienne de 2 plans :
Ax + by + cz + d = 0
a'x + b'y + c'z + d' = 0

Comment Trouvons nous le vecteur directeur de cette droite ?

[Kugge]

Bien entendu (a,b,c) ≠ (0,0,0) ≠ (a',b',c')

[GaBuZoMeu]

Par exemple, en faisant le produit vectoriel de deux vecteurs orthogonaux aux plans (directement donnés par les équations).

[mathelot]

bonsoir,
je pense que l'on doit considérer deux vecteurs normaux aux plans:
et

puis un vecteur normal à 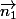et
(produit vectoriel)

[Kugge]

Par exemple, en faisant le produit vectoriel de deux vecteurs orthogonaux aux plans (directement donnés par les équations).

C'est vrai, u(bc'-b'c,ac'-a'c,ab'-a'b) néanmoins il n'y a aucune méthode plus directe et simple plus adaptée au lycee? j'imaginais quelque chose ressemblant au vecteur directeur d'une droite dans un plan (-b, a)

[Yezu]

Le produit vectoriel est la meilleure 'méthode' mais il me semble que niveau lycée on résout explicitement le système et on obtient une représentation paramétrique de la droite.