Variations d'une fonction, 1ère S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
saiyajin76
- Membre Naturel
- Messages: 45
- Enregistré le: 22 Sep 2007, 14:36
-
 par saiyajin76 » 12 Sep 2008, 18:39
par saiyajin76 » 12 Sep 2008, 18:39
Bonjour, j'ai besoin d'aide pour un DM qui me pose quelques problèmes...
f(x)=;)(x+2)
g(x)=;)(4x+8)
h(x)=2/x+2/ (valeur absolue de
il faut que je dise si fg=h. Mais je ne me souviens plus comment développer ;)x+2 X ;)4x+8 (oui je sais la honte en 1ere :we: ).
En essayant, je trouve ;)(x+2) X 2;)(x+2).
Il y aussi un autre exo qui me pose problème...
a) Etudier le sens de variation de la fonction x;)x+1/x sur ]0;+;)[
Pour ça, je prends deux réels a et b de ]0;+;)[ tels que aEnsuite je forme la différence entre f(a) et f(b) pour en étudier le signe. Je trouve (b-a)(ba+1)/ab mais la prof nous a dit qu'il fallait différencier deux cas: sur l'intervalle [0;1] puis [1;+;)[. Pourquoi?
b)a, b, c, d, e, f, g, h sont huit réels strictement positifs.
Démontrer l'inégalité suivante:
a/h + b/g + c/f + d/e + e/d + f/c + g/b + h/a ;)8
Pour ça, je n'ai aucune idée quant à la méthode.
Merci d'avance

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 12 Sep 2008, 21:33
par fatal_error » 12 Sep 2008, 21:33
Salut,
1:
T'as bien fait de tenter :++: , c'est juste, mais pas fini :
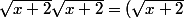^2=x+2)
2:pour le cas des intervalles. La prof vous a dit de différencier les cas car la fonction n'est peut etre pas monotone. SI ca se fait elle est croissante sur ]0;1] et decroissante sur
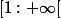
Le plus simple c'est de dériver ta fonction f:x->x+1/x et de regarder son signe.
3:Tu peux grouper les

fractions deux à deux ainsi (a/b et b/a) idem pour les autres. Que dire de a/b+b/a?
la vie est une fête

-
saiyajin76
- Membre Naturel
- Messages: 45
- Enregistré le: 22 Sep 2007, 14:36
-
 par saiyajin76 » 13 Sep 2008, 13:06
par saiyajin76 » 13 Sep 2008, 13:06
Salut,
1) Je ne comprends pas comment tu fais pour passer de ce que je j'ai fait à x+2, alors qu'il faut que je trouve 2|x+2|. Tu pourrais expliquer?
2)Je ne sais pas du tout ce que c'est de dériver une fonction. Pour les intervalles, j'ai vérifié sur géoplan, c'est vrai que la fonction n'est pas monotone (elle est décroissante sur [0;1] et croissante sur [1;+;)[ ). Pour le démontrer par le calcul, je prends deux réels de chaque intervalle ([0;1] et [1;+;)[ ) a et b tels que aa donc b-a>0
a>0 et b>0 donc ab>0
ab>-1 donc ab+1>0
Donc, f(a)-f(b)>0 donc f(a)>f(b).
Donc f est décroissante sur [0;1].
Ici aucun problème, j'ai trouvé ce que je voulais démontrer
2ème cas: Sur [1;+;)[
f(a)-f(b)= a + 1/a - (b + 1/b) = ba²+b-ab²-a/ab = (b-a) (ba+1)/ab
b>a donc b-a>0
a>0 et b>0 donc ab>0
ab>-1 donc ab+1>0
Donc, f(a)-f(b)>0 donc f(a)>f(b).
Donc f est décroissante sur [1;+;)[
C'est forcément faux, puisque la fonction est censée être décroissante sur cet intervalle. D'où viens le problème? De ma factorisation ou de mon raisonnement pour trouver le signe de f(a)-f(b)? Je ne sais pas.
Merci d'avance
-
saiyajin76
- Membre Naturel
- Messages: 45
- Enregistré le: 22 Sep 2007, 14:36
-
 par saiyajin76 » 13 Sep 2008, 13:42
par saiyajin76 » 13 Sep 2008, 13:42
pas de réponse?
-
saiyajin76
- Membre Naturel
- Messages: 45
- Enregistré le: 22 Sep 2007, 14:36
-
 par saiyajin76 » 13 Sep 2008, 14:22
par saiyajin76 » 13 Sep 2008, 14:22
up :help:
-
saiyajin76
- Membre Naturel
- Messages: 45
- Enregistré le: 22 Sep 2007, 14:36
-
 par saiyajin76 » 13 Sep 2008, 16:41
par saiyajin76 » 13 Sep 2008, 16:41
C'est bon, j'ai trouvé tout seul, on est jamais mieux servi que par soi-même... Merci à fatal_error qui m'a aidé
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
