Variations Suites

[Cameliaa.rose-xO]

Bonjour tout le monde (:
Voici quelques exos pour lesquels j'aimerai avoir une petite piste(pour le 1)^^
1)Soit f la fonction f(x) =
Déterminer son ensemble de déf puis ses variations sur Df.

2) Soit g la fonction g(x) =
Déterminer son ensemble de déf puis ses variations sur Dg.
Retrouver la réponse avec la dérivée de f(g)

3)Soit f la fonction f(x) =
déterminer son ensemble de définition Df puis ses variations sur Df.
Merci encore =]

[Cauchy-Ito]

Bonjour tout le monde (:
Voici quelques exos pour lesquels j'aimerai avoir une petite piste(pour le 1)^^
1)Soit f la fonction f(x) =
Déterminer son ensemble de déf puis ses variations sur Df.

2) Soit g la fonction g(x) =
Déterminer son ensemble de déf puis ses variations sur Dg.
Retrouver la réponse avec la dérivée de f(g)

3)Soit f la fonction f(x) =
déterminer son ensemble de définition Df puis ses variations sur Df.
Merci encore =]

Bonjour pour la première:

Une racine carrée est définie si la quantité sur la racine est > ou = 0 Donc tu dois avec l'aide d'un tableau de signe déterminer les valeurs de x pour lesquelles la quantité X^2-2x-3 est positive...Pour les variations étudies le signe de la dérivée :lol3: ...

[Cameliaa.rose-xO]

Bonjour pour la première:

Une racine carrée est définie si la quantité sur la racine est > ou = 0 Donc tu dois avec l'aide d'un tableau de signe déterminer les valeurs de x pour lesquelles la quantité X^2-2x-3 est positive...Pour les variations étudies le signe de la dérivée :lol3: ...

D'accord merci =)
Alors du coup j' obtiens X^2-2x-3>=0
Df = ]-inf ; - 1 ] U [3 +inf [

La dérivée de f(x) :
f'(x)= 2x-2
Sur -inf ; 1] la dérivée est négative et sur [1 + inf elle est positive ?

[Cauchy-Ito]

D'accord merci =)
Alors du coup j' obtiens X^2-2x-3>=0
Df = ]-inf ; - 1 ] U [3 +inf [

La dérivée de f(x) :
f'(x)= 2x-2
Sur -inf ; 1] la dérivée est négative et sur [1 + inf elle est positive ?

Non il ya une racine..

(racine(U))'= U'/2*racine(U)

Ex racine(X^3))'= 3x^2/2*racine(X^3)

[Cameliaa.rose-xO]

Non il ya une racine..

(racine(U))'= U'/2*racine(U)

Ex racine(X^3))'= 3x^2/2*racine(X^3)

Ok =] alors la dérivée est 2x-2 / 2x* rac x² - 2x-3 plutôt? et les variations étaient correct ?

[MacManus]

Ok =] alors la dérivée est 2x-2 / 2x* rac x² - 2x-3 plutôt? et les variations étaient correct ?

Bonjour.

Pour l'ensemble de définition, c'est correct :
En revanche, le calcul de la dérivée n'est pas tout à fait ce que tu donnes.
Reprenons la formule :
est dérivable sur , pour tout , on a
(ne pas oublier la multiplication par la constante devant la racine). Il est d'ailleurs possibe de simplifier cette expression.


EDIT !

[Cameliaa.rose-xO]

Bonjour.

Pour l'ensemble de définition, c'est correct :
En revanche, le calcul de la dérivée n'est pas tout à fait ce que tu donnes.
Reprenons la formule :
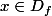
est définie et dérivable sur , pour tout , on a
(ne pas oublier la multiplication par la constante devant la racine). Il est d'ailleurs possibe de simplifier cette expression.

?

Pour le 2) l'ensemble de définition est donc le même :
en revanche pour la dérivée la formule à utiliser c'est bien u'/v'?

[Cauchy-Ito]

?

Pour le 2) l'ensemble de définition est donc le même :
en revanche pour la dérivée la formule à utiliser c'est bien u'/v'?

Il serait peut être judicieux que vous ouvriez votre cours avant de poster..vous ne maitrisez pas les bases...
Comment la 1 et 2 peuvent avoir le même Df (l'une est une racine et l'autre un quotient) :hum: ? et comment (u/v)'=u'/v'???

(u/v)'=(u'v-uv')/v^2

[Cameliaa.rose-xO]

Il serait peut être judicieux que vous ouvriez votre cours avant de poster..vous ne maitrisez pas les bases...
Comment la 1 et 2 peuvent avoir le même Df (l'une est une racine et l'autre un quotient) :hum: ? et comment (u/v)'=u'/v'???

(u/v)'=(u'v-uv')/v^2

D'accord, mais pour la 2) on a bien un quotient donc le dénominateur doit être différent de 0 ?
on a donc x² -2x-3# 0 ?

[Cauchy-Ito]

D'accord, mais pour la 2) on a bien un quotient donc le dénominateur doit être différent de 0 ?
on a donc x² -2x-3# 0 ?

Oui et alors?
Vous avez écris D_f = ]-\infty;-1[ \cup ]3;+\infty[ !!! Or par ex prenons la valeur 1 qui n'est pas dans le DF
et remplaçons dans x² -2x-3 on a: 1^2-2*1-3= -4 ce qui est bien different de 0.. Donc 1 appartient au Df.. Vous avez fait une erreur qqpart..

[Cameliaa.rose-xO]

Oui et alors?
Vous avez écris D_f = ]-\infty;-1[ \cup ]3;+\infty[ !!! Or par ex prenons la valeur 1 qui n'est pas dans le DF
et remplaçons dans x² -2x-3 on a: 1^2-2*1-3= -4 ce qui est bien different de 0.. Donc 1 appartient au Df.. Vous avez fait une erreur qqpart..

Euh Df= R \ { -1 ; 3 } ? :/

[Cauchy-Ito]

Euh Df= R \ { -1 ; 3 } ? :/

Oui!!!!
voilà!!