Variation d'une fonction

[Illups]

Bonjour,

Admettons qu'il y ait une fonction d'(x) = e^-x (x^2 - 2x - 1) et on veut grâce à cela trouver les variations de d.

Pourquoi on n'étudie pas le signe e^-x mais seulement de x^2 - 2x - 1 ? e^-x est positif, mais pourquoi plus

précisément ?

Pourquoi les abscisses données par x^2 - 2x - 1 correspondent à l'ensemble de la fonction dérivé d'(x) = e^-x

(x^2 - 2x - 1) quand on fait le tableau de variation ?

Je vous remercie d'avance.

[Pisigma]

Bonjour,


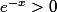
en appliquant la règle des signes au produit des 2 facteurs;

aura le signe de

puisque

[hdci]

Bonjour,

Pourquoi on n'étudie pas le signe e^-x mais seulement de x^2 - 2x - 1 ? e^-x est positif, mais pourquoi plus précisément ?

Quelle est votre question plus précisément : pourquoi n'étudie-t-on pas le signe de (sachant qu'il est positif...) ou pourquoi ?

Si c'est le premier cas, la réponse est trivial, non ? "quel est le signe de X sachant que X est positif..."
Si c'est le second cas, dans ce cas je vous renvoie sur votre cours : quel est le signe de l'exponentielle ? Vous avez forcément vu cela dans le cours, soit en "admis", soit démontré par votre professeur (la démonstration reposant sur le fait que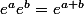 donc en particulier or et un carré est toujours positif, donc et l'inégalité est stricte car de la même façon ce qui fait que admet un inverse, donc ne peut être nul)

Le fait qu'on écrive ne change rien à l'histoire : si 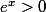pour tout réel , comme est également un réel, e^{-x} est donc strictement positif.

Pourquoi les abscisses données par x^2 - 2x - 1 correspondent à l'ensemble de la fonction dérivé d'(x) = e^-x
(x^2 - 2x - 1) quand on fait le tableau de variation ?

Cette phrase n'a aucun sens, pouvez-vous la préciser ?