Bonjour,
Soient n et d appartenants aux naturels non nuls, X une variable aléatoire suivant la loi uniforme sur
{1, . . . . . . , n}. Soit R la variable aléatoire égale au reste de la division euclidienne de X par d. Donner la loi de R.
Merci par avance.
Variable aléatoire et division euclidienne
6 messages
- Page 1 sur 1
Re: Variable aléatoire et division euclidienne
Salut,
Prend un exemple :
On tire au pif (et avec équiprobabilité) un jeton numéroté entre 1 et 10 (compris).
Quels sont les valeurs possibles pour le reste de la division par 3 ?
Quelle est la proba. de chaque valeur possible de ce reste ?
Prend un exemple :
On tire au pif (et avec équiprobabilité) un jeton numéroté entre 1 et 10 (compris).
Quels sont les valeurs possibles pour le reste de la division par 3 ?
Quelle est la proba. de chaque valeur possible de ce reste ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Variable aléatoire et division euclidienne
Salut Ben Kenobi,
Bonne idée de rétrécir l'intervalle afin de comprendre le mécanisme. Merci.
Bonne idée de rétrécir l'intervalle afin de comprendre le mécanisme. Merci.
Re: Variable aléatoire et division euclidienne
Monsieur Ben,
Corrige moi si je me trompe. . .
Soit P(X=Xi) avec i appartenant à {1, . . . . . . ., n}
La loi de R serait définie par :
R(Omega) = {0 ,1 , 2, . . . , n}
P(R=k)= (q+1)/n (si Xi=k car quotient nul) + P(R=k) = q/n (avec Xi>k et q de Xi=Xn pour faire apparaître les q occurrences de R=k)
Corrige moi si je me trompe. . .
Soit P(X=Xi) avec i appartenant à {1, . . . . . . ., n}
La loi de R serait définie par :
R(Omega) = {0 ,1 , 2, . . . , n}
P(R=k)= (q+1)/n (si Xi=k car quotient nul) + P(R=k) = q/n (avec Xi>k et q de Xi=Xn pour faire apparaître les q occurrences de R=k)
Re: Variable aléatoire et division euclidienne
Çà a plus ou moins l'air d'être ça, mais c'est franchement pas clair ton truc :
- Déjà ta variable aléatoire X, elle prend ces valeurs dans {1..n} donc je vois pas trop ce que c'est que tes . Ce que tu as, c'est, pour tout
. Ce que tu as, c'est, pour tout 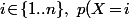\!=\!\frac{1}{n}) (loi uniforme sur {1..n}).
(loi uniforme sur {1..n}).
- Ensuite, je ne vois pas ce que représentent ton et ton
et ton  . Je suppose que c'est le quotient et le reste de la division euclidienne de
. Je suppose que c'est le quotient et le reste de la division euclidienne de  par
par  , mais il faudrait évidement l'écrire !!!
, mais il faudrait évidement l'écrire !!!
- Les valeurs que peut prendre , ça pourrait effectivement être {0..n} si on avait d>n, mais dans ce cas, ça n'aurait pas grand intérêt vu qu'on aurait R=X systématiquement (si on divise un entier X par un entier d>X, il y va 0 fois et il reste X). Donc les valeurs que prend R, c'est plutôt 0,1,2,...,d-1, c'est à dire l'ensemble des restes possibles d'une division euclidienne par d.
, ça pourrait effectivement être {0..n} si on avait d>n, mais dans ce cas, ça n'aurait pas grand intérêt vu qu'on aurait R=X systématiquement (si on divise un entier X par un entier d>X, il y va 0 fois et il reste X). Donc les valeurs que prend R, c'est plutôt 0,1,2,...,d-1, c'est à dire l'ensemble des restes possibles d'une division euclidienne par d.
- Enfin, pour un fixé, pour évaluer la proba. que
fixé, pour évaluer la proba. que  soit égal à
soit égal à  , il faut bien sûr compter combien il y a de
, il faut bien sûr compter combien il y a de 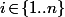 tels que le reste de la division de
tels que le reste de la division de  par
par  soit égal à
soit égal à  . Un tel
. Un tel  doit donc s'écrire
doit donc s'écrire 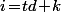 pour un certain entier
pour un certain entier  et il faut donc compter le nombre d'entier
et il faut donc compter le nombre d'entier  tels que
tels que  . Si on reprend la division euclidienne
. Si on reprend la division euclidienne 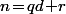 l'encadrement s'écrit
l'encadrement s'écrit  .
.
Si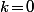 on obtient
on obtient  c'est à dire
c'est à dire  vu que
vu que  doit être entier. Il y a donc donc
doit être entier. Il y a donc donc  possibilités et on a
possibilités et on a 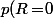\!=\!\dfrac{q}{n})
Je te laisse finir de traiter les autres cas où il y a deux cas de figure selon que ou pas.
ou pas.
Et tu vérifia tes résultats sur l'exemple n=10; d=3 où on a p(R=0)=3/10; p(R=1)=4/10 ; p(R=2)=3/10.
- Déjà ta variable aléatoire X, elle prend ces valeurs dans {1..n} donc je vois pas trop ce que c'est que tes
- Ensuite, je ne vois pas ce que représentent ton
- Les valeurs que peut prendre
- Enfin, pour un
Si
Je te laisse finir de traiter les autres cas où il y a deux cas de figure selon que
Et tu vérifia tes résultats sur l'exemple n=10; d=3 où on a p(R=0)=3/10; p(R=1)=4/10 ; p(R=2)=3/10.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Variable aléatoire et division euclidienne
Reprenons l'exemple (avec n=10 et d=3) pour comprendre et prouver que les deux cas figures sont une réunion disjointe :
X=1= 3 x 0 + 1
X=2= 3 x 0 +2
X=3= 3 x 1 + 0
X=4= 3 x 1 + 1
X=5= 3 x 1 +2
X=6= 3 x 2 + 0
X=7= 3 x 2 + 1
X=8= 3 x 2 +2
X=9= 3 x 3 + 0
X=10= 3 x 3 + 1
On retrouve bien P(R=0)=3/10, P(R=1)=4/10 et P(R=2)=3/10
Peux-tu donc clarifier, en application numérique, k et r ? t ne peut pas être égale à 0 (cf X=1 et X=2)?
X=1= 3 x 0 + 1
X=2= 3 x 0 +2
X=3= 3 x 1 + 0
X=4= 3 x 1 + 1
X=5= 3 x 1 +2
X=6= 3 x 2 + 0
X=7= 3 x 2 + 1
X=8= 3 x 2 +2
X=9= 3 x 3 + 0
X=10= 3 x 3 + 1
On retrouve bien P(R=0)=3/10, P(R=1)=4/10 et P(R=2)=3/10
Peux-tu donc clarifier, en application numérique, k et r ? t ne peut pas être égale à 0 (cf X=1 et X=2)?
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
