Valeur moyenne d'une fonction continue

[glois]

Salut et merci pour votre aide
f est une fonction continue sur un intervalle fermé borne'I d'extrémité a et b et telle que f et f^2 ont la même valeur moyenne .
Montrer que la fonction f est constante sur l'intervalle I.

[glois]

Salut et merci pour votre aide
f est une fonction continue sur un intervalle fermé borne'I d'extrémité a et b et telle que f et f^2 ont la même valeur moyenne .
Montrer que la fonction f est constante sur l'intervalle I.

[lyceen95]

Tu es sûr d'avoir correctement noté l'énoncé de l'exercice ?
Je pense qu'il est assez simple de bâtir un contre exemple : une fonction f, qui vérifie les hypothèses, et qui n'est pas constante.

[glois]

Oui ce sont exacts les énoncés, merci de m,en donner un contre exemple

[Carpate]

Il y a au moins 2 fonctions constantes qui répondent à ces conditions .
f continue sur un intervalle




En effet formellement :

[glois]

Merci bien mais il s'agit du cas général

[Carpate]

Qu'est-ce que tu veux dire par cette remarque :

Merci bien mais il s'agit du cas général

Du fait de l'équivalence que j'ai mentionnée au début des calculs, ces 2 fonctions constantes sont les 2 seules répondant à la question.

@ lycéen95

Je pense qu'il est assez simple de bâtir un contre exemple : une fonction f, qui vérifie les hypothèses, et qui n'est pas constante.

Merci de fournir une telle fonction .

[Rdvn]

Bonjour
I=[0,1]
f définie sur I par f(x) = (3/2)*x
f remplit les conditions sans être constante

[Carpate]

Bonjour,
Au temps pour moi !
J'ai mal interprété l'énoncé, ma réponse concernait les fonctions et 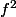qui ont même valeur moyenne sur tout intervalle de leur domaine de définition (commun).
Sur [0;1], et pourtant leur valeur moyenne est la même.
Ce n'est pas graphiquement intuitif !
As-tu trouvé cet exemple au hasard où as-tu une méthode pour les rechercher ?
Merci.

[Rdvn]

Bonsoir
Je me suis placé sur [0,1] en me disant que je cherchais un contre exemple, et que, à priori,
fixer un intervalle particulier ne changerait rien.
La deuxième idée c'est d'interpréter les intégrales comme aire :
pour k>1 la courbe d'équation y = (kx)^2 est tantôt au dessus tantôt en dessous de la droite
d'équation y=kx , d'où l'idée d'ajuster k .
Si on note Int (f(x)) l'intégrale de 0 à 1 de f(x) :
In(kx)=kInt(x)
Int((kx)^2)=k^2Int(x^2)
On ajuste k
Cordialement

[lyceen95]

Et moi, j'avais en tête la fonction f(x)=x.
Sur l'intervalle [0,1], l'intégrale de f² est inférieure à l'intégrale de f.
Sur l'intervalle [0,2], c'est l'inverse, l'intégrale de f² est supérieure à l'intégrale de f.
Donc, il y a un intervalle [0,b] , avec b entre 1 et 2, où ces 2 intégrales sont égales.

Peut-être qu'on se plante sur la lecture de l'exercice , f² signifierait f o f ?
Mais même dans ce cas, la propriété proposée est fausse, la fonction f(x)=x est un contre-exemple.

[hdci]

Peut-être que l'énoncé devrait être "sur tout intervalle, les deux fonctions ont même valeur moyenne" ?

[Rdvn]

Bonjour à tous,
Je viens de relire l'énoncé : il parle bien d'une fonction définie sur un intervalle, donc à priori tout ceci est fixé.
Maintenant si il s'agissait de fof il y avait des précisions à apporter...
Enfin bref c'est un énoncé bancal, pour ma part j’arrête là
Bonne journée