Urgent

[nounours94170]

Bonjour a tous,
j'ai un gros problème je dois rendre mon devoir pour demain, et je n'arrive vraiment pas, pourriez vous m'aider svp ?
Voila lénoncé :
1)Soit I(n )= (Intégralle de 0 à 1) (x^n*(e^-x))dx
Démontrer que le nombre In existe pour tout n, appartenant à N* et qu'il est positif. Calculer I1

j'ai penser à utiliser la positivité , en montrant que comme n appartient à N* on peut dire que il est positif, de plus elle est constitué de deux fonctions stricment positive sur l'intervalle . nan ?

2) Démontrer que pour tout n appartenant à N* on a :
I(n+1)= - 1/e + ( n+1 ) * I(n)

Il faut que j'utilise une intégration par parties, mais je n'arrive pas..
calculer I2 et I3

Aidez moi svp, merci d'avance
Cordialement .

[euclide]

Pour la première question il faut montrer que est une fonction continue sur l'intervalle [0,1] pour tout n (pour montrer que existe pour tout n). Pour montrer la positivité tu as raison il faut montrer que f est une fonction positive sur [0,1] pour tout n. Et pour caluler 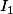, tu peux faire une intégration par partie en prenant et .

Pour la seconde question il faut faire la même intégration par partie mais dans le cas général tu calcul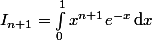 et tu trouveras la solution.

[nounours94170]

Merci beaucoup !!!
Bonne soirée

[Joker62]

HUm ça sent la factorielle ! :)