Coucou!
J'ai vraiment besoin d'aide svp pour un exercice, si vous pouvez répondre à cet SOS svp!
Une droite d coupe le cercle C de centre O et de rayon r en deux points A et B. [AA'] diamètre.
a) Pour tout point M de d situé à une distance d1 de O, décomposer (vecteur)MB à l'aide de A', montrer que (vecteurs) MA.MB=(MO+OA).(MO-OA), puis (vecteurs) MA.MB=d1²-r² [FONT=Arial Black]donc cette partie j'y suis arrivé[/FONT]
b) Les points A,B,C et D sont tels que (AB) et (CD) sont sécants en I. Démontrer que A, B, C et D sont cocycliques si et seulement si (vecteurs) IA.IB = (vecteurs) IC.ID
[FONT=Arial Black]lA J'Y ARRIVE PAS DU TOUT[/FONT] :hein:
Merci!!!! j'attends une réponse o plus vite svp!!! :happy2:
Urgent!!!! Help svp!
3 messages
- Page 1 sur 1
La démonstration dans un sens est assez simple.
Supposont A,B,C,D cocycliques.
Si O est le centre du cercle par lequel passe ABCD et r le rayon de ce cercle.
On a démontré dans le a) que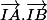 = d1² - r²
= d1² - r²
où d1 est la distance du point I au point O
Mais on a également = d1² - r², car le cercle est le même.
= d1² - r², car le cercle est le même.
On a donc démontré que :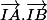 =
= 
Supposont A,B,C,D cocycliques.
Si O est le centre du cercle par lequel passe ABCD et r le rayon de ce cercle.
On a démontré dans le a) que
où d1 est la distance du point I au point O
Mais on a également
On a donc démontré que :
Dans l'autre sens, ca parait moins simple.
Je te fais quand même une proposition.
On fait l'hypothèse que :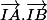 =
= 
Considérons le point O intersection des médiatrices des segments [AB] et [BC].
Soit r1 = d(O,A) = d(O,B) et soit r2 = d(O,C) = d(O,D)
Le cercle C1 de centre O et de rayon r1 passe par A et B.
Le cercle C2 de centre O et de rayon r2 passe par C et D.
On a démontré dans le a) que :
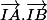 = d1² - r1²
= d1² - r1²
et
 = d1² - r2²
= d1² - r2²
où d1 est la distance de I à O.
Comme on a pour hypothèse :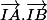 =
=  , on en déduit r1² = r2²
, on en déduit r1² = r2²
Les cercles C1 et C2 ont le même rayon et le même centre, donc C1 = C2.
On a démontré qu'il existe un cercle passant par les points A,B,C,D.
Je te fais quand même une proposition.
On fait l'hypothèse que :
Considérons le point O intersection des médiatrices des segments [AB] et [BC].
Soit r1 = d(O,A) = d(O,B) et soit r2 = d(O,C) = d(O,D)
Le cercle C1 de centre O et de rayon r1 passe par A et B.
Le cercle C2 de centre O et de rayon r2 passe par C et D.
On a démontré dans le a) que :
et
où d1 est la distance de I à O.
Comme on a pour hypothèse :
Les cercles C1 et C2 ont le même rayon et le même centre, donc C1 = C2.
On a démontré qu'il existe un cercle passant par les points A,B,C,D.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
