On considère la suite numérique
On considère la suite
Il m'est demander de démontrer que la suite
Pour cela je fais cette équation :
Je remplace pour
Après ça je ne sais pas comment continuer, merci de votre aide.
alex-blade2 a écrit:Si je vois il faut faire la forme conjugué, puis passer le 2 a gauche pour se ramener a une équation =0. Je vais essayer de faire pareil pour Vn je te tiens au courant. Mais une fois qu'on a Vn+1 en fonction de Vn comment peut-on conclure ?
Non, ici, ça ne sert à rien de "faire la forme conjuguée" car, sous les racines, ce sont des "vrais nombres" donc les racines "ne gènent pas.alex-blade2 a écrit:Si je vois il faut faire la forme conjugué
alex-blade2 a écrit:Bonjour(soir) à tous je vous demande de l'aide sur un exercice que je n'arrive pas à finir je vous donne l'énoncé et ce que j'ai trouvé :
On considère la suite numériquedéfinie par
et, pour tout entier n,
.
On considère la suitedéfinie pour tout entier n par

Il m'est demander de démontrer que la suiteest géométrique.
Pour cela je fais cette équation :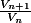
Je remplace pour,
par son expression, ensuite je réduis au même dénominateur je réduis et je trouve :
Après ça je ne sais pas comment continuer, merci de votre aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :