Une question sur les congruences...

[riversub]

Bonjour je suis en plein dans un dm de maths etje doute sur une réponse concernant les congruences.


La connaissance de l'énoncé sur le codage n'est pas requise je pense.

. Démontrer que si a et b sont 2 nombres entiers distincts tels que 0<=a<=25 et 0<=b<=25 , alors 19a n'est pas congru à 19b modulo 26.

Voici ce que je pensais mettre :
si a est différent de b
avec a et b dans [0 ; 25]
alors a n'est pas congru à b modulo 26
(la division de a et de b par 26 donne deux restes différents)
Et si on a 19a 19b (26)
Comme pgcd(19 ;26) = 1
a b (26) ce qui est faux par hypothèse

du coup c’est impossible d’avoir 19a 19b (26)


Justement je ne sais pas si l'on peut dire 19a 19b (26) et donc a b (26) car on m'a toujours dit que la division ne marchait pas pour les congruences.

[Nightmare]

Bonsoir,

Et si on a 19a 19b (26)
Comme pgcd(19 ;26) = 1
a b (26)

Oui c'est vrai, comment le justifies-tu ?

[riversub]

Bah justement je ne sais pas trop comment le justifier...


J'aurais donc aimé l'aide d'un membre plus expérimenté que moi...

[Nightmare]

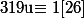
Le théorème de Bezout t'assures l'existence d'un u et d'un v tels que 19u+26v=1. On en déduit que (on dit que u est l'inverse de 19 modulo 26)

Ainsi, si
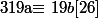
En multipliant par u :

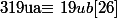
ie :
.

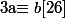
[riversub]

D'accord, j'ai compris, merci bien.

[Nightmare]

Je t'en prie !