Une question à propos des nombres complexes

[Burp]

Comment peut on montrer que si (z+2+3i)^5=(z-2+3i)^5 alors z est imaginaire?

[MJoe]

Comment peut on montrer que si (z+2+3i)^5=(z-2+3i)^5 alors z est imaginaire?

Bonjour,

Il suffit de montrer que la partie réelle du complexe est égale à 0.

s'écrit :

et

s'écrit :

On doit avoir égalité des modules de ces deux complexes, donc :








Donc et est imaginaire pur.

Autre manière de voir les choses :
Si on considère le point d'affixe et le point d'affixe . Le point d'affixe tel que appartient à la médiatrice de et cette médiatrice est l'axe des ordonnées du plan complexe. Donc est imaginaire pur.

MJoe

[Burp]

Merci <3

[MJoe]

Bonjour à tous,

mais que vaut ?

J'ai trouvé 4 solutions pour et donc pour :

;


;

MJoe.

[Razes]

On pose:

(Le cas 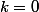n'est pas solution dans notre exercice car on trouverait que , ce qui est impossible, car )



Donc est imaginaire

[Pseuda]

Comment peut on montrer que si (z+2+3i)^5=(z-2+3i)^5 alors z est imaginaire?

Bonjour,

Encore une solution (sans chercher à résoudre l'équation) :



Donc, on a : .

On développe, on réduit, et on aboutit à : , donc z est imaginaire pur.

Pour info, en principe on dit que "imaginaire" = complexe non réel (, avec ), c'est différent de "imaginaire pur" (, ).