Une petite indice svp
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 05 Fév 2019, 21:44
par zerow2001 » 05 Fév 2019, 21:44
Salut !!!

Dans un exercice sur les nombres complexes ils ont dis :
a appartient à C
1) Verifier que : 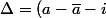^{2})
l'équation est :
Z-\bar{a}-ia\bar{a})
Pour moi, j'ai dejà fait l'exercice tous l'exercice, mais je suis curieux si la question étais "calculer" et pas verifiee, je veux quelqu'un qui peux m'aider à connaitre delta sans "verification" (PS : je peux calculer delta mais s'il est un peu simple comme (1+i)² ou bien (3+4i)².....
Merci pour votre temps et votre aide

-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Fév 2019, 11:06
par Carpate » 06 Fév 2019, 11:06
Ce qu'a voulu dire Zerow2001 c'est comment en partant de
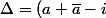^2+4(a+ia\bar{a}))
arriver à
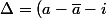^2)
L'auteur de l'énoncé a certainement utilisé la méthode générale suivante (mais je n'ai pas la motivation nécessaire pour aller au bout de ces calculs) :
Isoler partie réelle et imaginaire de

:
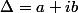
Chercher, par identification
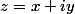
tel que
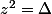
Cela donne :
(1)
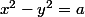
(2)
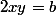
Un raccourci permet d'alléger les calculs :
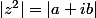
soit (2)' :
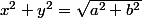
En combinant (1) et (2)' :
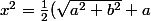)
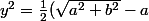)
puis x et y
bon courage ...
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 06 Fév 2019, 20:05
par zerow2001 » 06 Fév 2019, 20:05
Merci beacoup, j'ai compris maintenant, j'ai seulemnt besoin de faire plusieur exercices pour m'adapter MERCI !
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 07 Fév 2019, 08:46
par Pisigma » 07 Fév 2019, 08:46
Bonjour,
sauf erreur de ma part,
en tenant compte de
^2=a^2+b^2+c^2\pm 2ab\pm 2ac\pm 2bc)
et en calculant
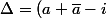^2+4\textcolor{red}{i}(\bar{a}+ia\bar{a}))
on trouve bien
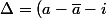^2)
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 07 Fév 2019, 10:13
par Pisigma » 07 Fév 2019, 10:13
autre piste moins "calculatoire"
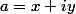
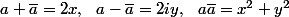
il faut montrer que
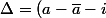^2=(2iy-i)^2)
, soit
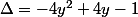
par calcul
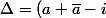^2+4i(\bar{a}+ia\bar{a})=(2x-i)^2+4i(x-iy)-4(x^2+y^2))
soit
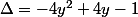
-
Black Jack
 par Black Jack » 07 Fév 2019, 11:33
par Black Jack » 07 Fév 2019, 11:33
Salut,
delta = (a + a(barre) - i)² - 4i(-a(barre) - i.a.a(barre))
delta = [a² + (a(barre))² - 1 + 2a.a(barre) - 2i.a - 2i.a(barre)] + 4i.a(barre) - 4.a.a(barre)
delta = a² + (a(barre))² - 1 - 2a.a(barre) - 2i.a + 2i.a(barre)
Or :
(a - a(barre) - i)² = a² + (a(barre))² - 1 - 2a.a(barre) - 2i.a + 2.i.a(barre)
--> delta = (a - a(barre) - i)²

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 07 Fév 2019, 12:07
par Pisigma » 07 Fév 2019, 12:07
Salut Blackjack
Au moins le posteur aura le choix
-
zerow2001
- Membre Relatif
- Messages: 199
- Enregistré le: 06 Jan 2019, 21:52
-
 par zerow2001 » 07 Fév 2019, 13:45
par zerow2001 » 07 Fév 2019, 13:45
J'ai aimé ta réponse Pisigma, vous pouvez dire que ce sujet est fermé
Merci beaucoup Black jack / Carpate / Sake
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 07 Fév 2019, 13:54
par Carpate » 07 Fév 2019, 13:54
@ Pisigma
Effectivement , je n'avais pas vu le

coefficient de

!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
