Une limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nisrina
- Membre Naturel
- Messages: 98
- Enregistré le: 11 Fév 2007, 19:21
-
 par Nisrina » 25 Fév 2007, 12:01
par Nisrina » 25 Fév 2007, 12:01
Bonjour
je bute encore sur une limite :
}}{x-1})
suffit-il juste de dire que c'est équivaut à
^x}{x-1})
et puisque x tends vers 1+ alors
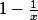
tend vers +oo
donc ca td vers +oo ?,?
est-ce ça ?
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Fév 2007, 12:11
par Nicolas_75 » 25 Fév 2007, 12:11
Bonjour,
Quelle propriété du cours utilises-tu pour justifier "donc ca" ?
Nicolas
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Fév 2007, 12:24
par Nicolas_75 » 25 Fév 2007, 12:24
Elle m'a l'air corsée....
Est-ce vraiment une limite de Terminale ? :hein:
-
Nisrina
- Membre Naturel
- Messages: 98
- Enregistré le: 11 Fév 2007, 19:21
-
 par Nisrina » 25 Fév 2007, 13:02
par Nisrina » 25 Fév 2007, 13:02
salut Nicolas ,
Quelle propriété du cours utilises-tu pour justifier "donc ca" ?
je ne suis pas sure mais si :
x td vers 1+ et
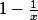
td vers +oo alors
^x)
tends vers +oo (c là ou je ne suispas sure !)
et on a x-1 td vers 0+ donc
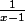
tends vers +oo
+oo x +oo = +oo donc ça diverge vers +oo
non ?
-
nxthunder
- Membre Relatif
- Messages: 224
- Enregistré le: 30 Juin 2005, 09:16
-
 par nxthunder » 25 Fév 2007, 13:25
par nxthunder » 25 Fév 2007, 13:25
Nisrina a écrit:salut Nicolas ,
je ne suis pas sure mais si :
x td vers 1+ et
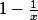
td vers +oo
non ?
Depuis quand
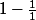
tend vers

1-1 = 0 sauf preuve du contraire . . .
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 25 Fév 2007, 14:22
par MacErmite » 25 Fév 2007, 14:22
moi aussi j'ai envie de délirer :marteau:
}}{x-1}=\frac{(1-\frac{1}{x})^x}{x-1}= (\frac{x-1}{x})^x.\frac{1}{x-1}=(x-1)^x.(x-1)^{-1}.x^{-x}=(x-1)^{x-1}.x^{-x})
donc cette limite tend vers 1 ? :doh:
-
Nisrina
- Membre Naturel
- Messages: 98
- Enregistré le: 11 Fév 2007, 19:21
-
 par Nisrina » 25 Fév 2007, 14:33
par Nisrina » 25 Fév 2007, 14:33
oui je délirais :briques: je sais pas à quoi j'étais entrain de penser , désolée!
---MacErmite :
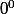
est une forme indéterminée (sauf erreur) !
^{x-1})
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 25 Fév 2007, 14:47
par MacErmite » 25 Fév 2007, 14:47
Je ne connais pas les règles des limites, ou du moins j'ai oublié. En effet
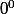
est inderterminé.
J'ai fini par faire cela :
^{1,001-1}.1,001^{-1,001}=0,99...)
pardonné moi mon père car j'ai péché ... délivré moi de la calculatrice ...
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Fév 2007, 14:51
par Nicolas_75 » 25 Fév 2007, 14:51
Attention :
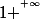
est une forme indéterminée.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 25 Fév 2007, 15:07
par Joker62 » 25 Fév 2007, 15:07
Cette limite ne serait-elle pas en faite la limite du taux d'accroissement de la fonction (1-(1/x))^x ??? :)...
Le problème ça restera quand même de calculer la dérivée lol :D
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Fév 2007, 15:08
par Nicolas_75 » 25 Fév 2007, 15:08
Est-elle dérivable ? :doh:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Fév 2007, 15:58
par Nightmare » 25 Fév 2007, 15:58
Bonjour à tous.
C'est vrai qu'elle ne m'a pas l'air évidente...
A coup de développement limité ça ne peut pas marcher?
-
Nicolas_75
- Membre Rationnel
- Messages: 919
- Enregistré le: 29 Aoû 2005, 11:42
-
 par Nicolas_75 » 25 Fév 2007, 16:01
par Nicolas_75 » 25 Fév 2007, 16:01
Salut Nightmare. Pour ma part, Morphée m'attend. Bon courage. Je doute qu'elle te résiste bien longtemps (pas Morphée, mais la limite).
Cordialement,
Nicolas
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Fév 2007, 16:02
par Nightmare » 25 Fév 2007, 16:02
Salut Nicolas :happy3:
Moi c'est le cinéma qui m'attend, donc la limite devra attendre encore un peu :lol3:
:happy3:
-
Nisrina
- Membre Naturel
- Messages: 98
- Enregistré le: 11 Fév 2007, 19:21
-
 par Nisrina » 25 Fév 2007, 19:15
par Nisrina » 25 Fév 2007, 19:15
Joker62 a écrit:Cette limite ne serait-elle pas en faite la limite du taux d'accroissement de la fonction (1-(1/x))^x ???

...
Le problème ça restera quand même de calculer la dérivée lol

la question de départ était d'étudier la dérivabillité à droite de 1 de
^x)
!
Nightmare -- j'ai pas encore vu de DL .
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Fév 2007, 19:25
par Nightmare » 25 Fév 2007, 19:25
Je l'ai...
On pose

On cherche donc la limite quand u tend vers 0 de :
ln\(1-\frac{1}{u+1}\)}}{u})
ie de :
ln(u)}}{u}\times e^{-(u+1)ln(u+1)})
Le facteur de droite tend vers 1, il va s'agir de montrer que celui de gauche aussi.
ln(u)}=e^{uln(u)}\times e^{ln(u)}=e^{uln(u)}\times u)
En divisant par u :
ln(u)}}{u}=e^{uln(u)})
On sait que uln(u) tend vers 0 lorsque u tend vers 0 (croissance comparée) donc
}=e^{0}=1)
Finalement :
ln(u)}}{u}\times e^{-(u+1)ln(u+1)}=1\times 1=1)
La fonction est bien dérivable en 1 et son nombre dérivée en 1 vaut 1.
-
Nisrina
- Membre Naturel
- Messages: 98
- Enregistré le: 11 Fév 2007, 19:21
-
 par Nisrina » 25 Fév 2007, 19:40
par Nisrina » 25 Fév 2007, 19:40
Great Nightmare :++:
merci bien :we: (juste pour la conclusion la fonction est dérivable en 1+ )
Bonne soirée !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Fév 2007, 19:41
par Nightmare » 25 Fév 2007, 19:41
De rien :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités