Bonjour, mon professeur de mathématiques m'a donné un exercice que je n'arrive pas a faire, est ce que vous pouvez m'aider?
Un+1=(Un)^2 +Un
-1/2>U1>0
montrez par récurrence que pour tout n€N
-1/(1+n)<Un<0
Merci d'avance.
Une inégalité par recurrence
6 messages
- Page 1 sur 1
Re: Une inégalité par recurrence
Salut,
Il y a peut-être plus rapide, mais personnellement, je ferais une mini étude de la fonction sur
sur  pour voir ce qu'on peut dire de
pour voir ce qu'on peut dire de 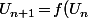) lorsque l'on sait que
lorsque l'on sait que  avec
avec  .
.
Il y a peut-être plus rapide, mais personnellement, je ferais une mini étude de la fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une inégalité par recurrence
Ben314 a écrit:Salut,
Il y a peut-être plus rapide, mais personnellement, je ferais une mini étude de la fonctionsur
pour voir ce qu'on peut dire de
lorsque l'on sait que
avec
.
Merci mais je DOIS le faire par récurrence même si c'est plus long
Re: Une inégalité par recurrence
Faire des déduction du style "Si  est comme çi alors
est comme çi alors  est comme ça", tu appelle ça comment toi ?
est comme ça", tu appelle ça comment toi ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Une inégalité par recurrence
Bonjour
Juste une remarque quand on doit manipuler des inégalités il vaut mieux avoir des formes canoniques (c'est à dire contenant une seule fois la variable, ici .
.
Donc utiliser la définition sous cette forme :
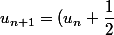^2-\dfrac{1}{4})
Pour illustrer, utilisons ceci pour encadrer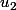
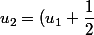^2-\dfrac{1}{4})
Or
donc

puis
^2<\dfrac{1}{4})
et enfin
^2-\dfrac{1}{4}<0)
donc
 car
car 
le cas général (de n à n+1) peut se traiter de cette façon...
Juste une remarque quand on doit manipuler des inégalités il vaut mieux avoir des formes canoniques (c'est à dire contenant une seule fois la variable, ici
Donc utiliser la définition sous cette forme :
Pour illustrer, utilisons ceci pour encadrer
Or
donc
puis
et enfin
donc
le cas général (de n à n+1) peut se traiter de cette façon...
Re: Une inégalité par recurrence
Il y a une erreur dans l'énoncé, c'est (probablement) : -1/2<U1<0 et non -1/2>U1>0
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
