Un problème d'un autre forum:
La fonction
Cordialement,
Dacu
aviateur a écrit:Bonjour
Dacu a écrit:aviateur a écrit:Bonjour
Bonjour,
Je dis que.Il est correct?
Cordialement,
Dacu
beagle a écrit:Dacu a écrit:aviateur a écrit:Bonjour
Bonjour,
Je dis que.Il est correct?
Cordialement,
Dacu
non?
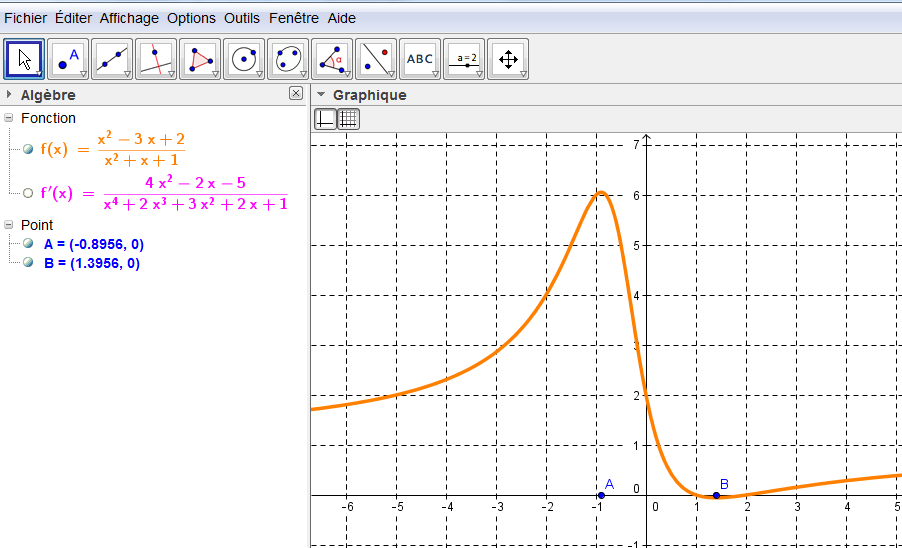
MJoe a écrit:Bonjour,
Pour terminer mon post,est bien l'ensemble cherché. Donc c'est correct.
MJoe.
MJoe a écrit:Bonjour,
Oui mais icin'a pas d'antécédent par
. C'est cela qui me gène !
On a :et
MJoe.
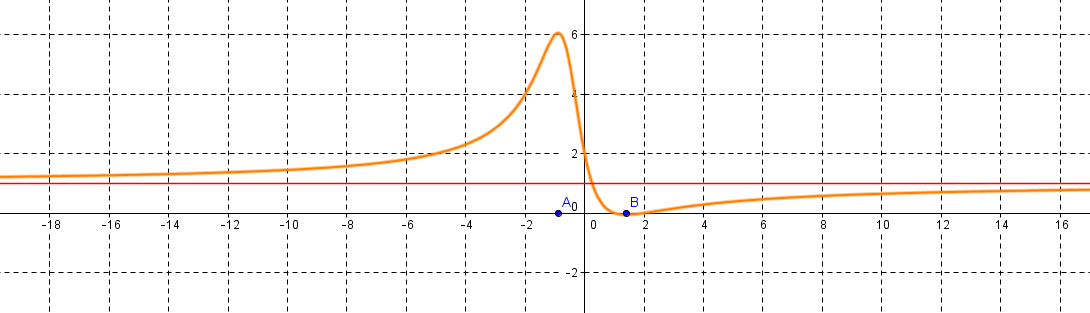
zygomatique a écrit:salut
mais bon sang il suffit de regarder le dessin pour voir que 1 a évidemment un antécédent
f est donc surjective de R sur [y(B), y(A)] = E
et les réels y(B), 1 et y(A) n'ont qu'un antécédent alors que les autres en ont deux ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :