Une dérivée me manque!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tinalopez
- Membre Naturel
- Messages: 36
- Enregistré le: 07 Fév 2007, 16:26
-
 par tinalopez » 30 Avr 2007, 10:20
par tinalopez » 30 Avr 2007, 10:20
On considère la fonction numérique f définie sur [0, +linfini ] par
f(t)=1000(0,8)^t
a) étudier les variation de f sur [0, +linfini ] et sa limite en + linfini
mais je n'arrive pas à dériver cette fonction...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 30 Avr 2007, 10:48
par Flodelarab » 30 Avr 2007, 10:48
Quel est la définition d'un exposant réel ?
Une fois que tu as traduit, montre nous tes étapes de calculs.
-
andros06
- Membre Relatif
- Messages: 180
- Enregistré le: 30 Aoû 2006, 13:30
-
 par andros06 » 30 Avr 2007, 10:56
par andros06 » 30 Avr 2007, 10:56
une petite aide :
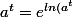}=e^{ln(a).t})
avec a>0
-
tinalopez
- Membre Naturel
- Messages: 36
- Enregistré le: 07 Fév 2007, 16:26
-
 par tinalopez » 30 Avr 2007, 11:11
par tinalopez » 30 Avr 2007, 11:11
f(t)=1000(0,8)^t
donc f(t)= 1000 e^(ln(0,8)t))
ah oui, j'ai une formule donc c'est :
f'(t)=1000 * (0,8)^t * ln(0,8)
non ?
et de plus comme 0,8 est compris entre 0 et 1 la fonction est décroissante sur l'intervalle
c'est ça ?? :hein:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 30 Avr 2007, 11:29
par Flodelarab » 30 Avr 2007, 11:29
Oui
:++: tout bon
-
tinalopez
- Membre Naturel
- Messages: 36
- Enregistré le: 07 Fév 2007, 16:26
-
 par tinalopez » 30 Avr 2007, 11:42
par tinalopez » 30 Avr 2007, 11:42
merci :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
