Trouver une limite avec des logarithmes

[Julinee]

Bonjour,
j'ai un exercice à faire et je dois trouver la limite de f(x) = (3/x) + 2lnX
en 0+.

Le problème c'est que ça me donne une forme indéterminée. Donc j'essaye de faire un changement de variable : soit X = lnx, soit X = 1/x
seulement dans les deux cas, j'ai un X et un x, du coup je peux pas résoudre.

Quelqu'un pourrait-il m'éclairer ?

[Skullkid]

Bonjour, essaye d'utiliser les limites classiques dites de croissance comparée (lnx/x et compagnie).

[Julinee]

merci pour la réponse =)

Le problème c'est que je ne vois quelle formule utiliser à part lim(lnx) quand x tend vers 0+ est - l'infini.
Sinon il faudrait que je transforme f(x) pour avoir une auter formule ?

[Sa Majesté]

Oui il faut transformer f(x) pour utiliser des limites que tu as dû voir dans ton cours

[Skullkid]

Ce qu'il faut retenir c'est que la seule façon que tu connais de comparer entre eux x, ln(x) et exp(x) en cas de forme indéterminée, c'est les croissances comparées.

De façon non rigoureuse, ces limites classiques te disent que, par exemple en l'infini, exp(x) "gagne" devant n'importe quelle puissance de x, qui elle-même "gagne" devant ln(x). En gardant en tête ce principe, on peut se forger une intuition pour le calcul de certaines limites.

Ainsi, dans ton exemple, tu es face à 3/x + lnx. Intuitivement, comme les puissances de x l'emportent sur les logarithmes, on se dit que le terme qui va gagner est 3/x, et donc que la limite vaut . Reste à le prouver, et une manière simple de le faire est de factoriser par la quantité que l'on estime comme étant la quantité dominante. Soit ici 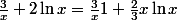. Et là tout de suite...