bonjour,
trouver tous les nombres entier n : pgcd(n-2,6)=1
Trouver tous les nombres entier n
6 messages
- Page 1 sur 1
Re: trouver tous les nombres entier n
Tuvasbien a écrit:Essaye d'appliquer le théorème de Bezout
Bonjour, puis je demander c'est quoi la theoreme de bezout? J'ai lu l'article wiki mais je ne comprennds pas bien
Re: trouver tous les nombres entier n
Si \in\mathbb{Z}^2) , alors
, alors  et
et  sont premiers entre eux si et seulement si il existe
sont premiers entre eux si et seulement si il existe \in\mathbb{Z}^2) tel que
tel que 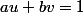 .
.
Re: trouver tous les nombres entier n
Bonsoir !
PGCD(n-2;6)=1<=> n-2≠6k, n-2≠2b, n-2≠3c
<=>n≠2(3k+1), n≠2(b+1), n≠3c+2, k, b et c étant des entiers naturels
Donc n est un nombre impair ne s'ecrivant pas sous la forme 3c+2
PGCD(n-2;6)=1<=> n-2≠6k, n-2≠2b, n-2≠3c
<=>n≠2(3k+1), n≠2(b+1), n≠3c+2, k, b et c étant des entiers naturels
Donc n est un nombre impair ne s'ecrivant pas sous la forme 3c+2
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
