Trouver un minimum
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 16 Déc 2013, 11:25
par Dante0 » 16 Déc 2013, 11:25
Bonjour,
Je dois trouver le minimum de la fonction :
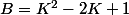
On sait que

Je dérive une première fois :
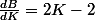
J'égalise à 0 :
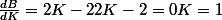
Dérivée seconde :
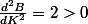
Mais je dois prouver que B admet un minimum en
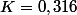
je fais comment ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 16 Déc 2013, 11:28
par Sylviel » 16 Déc 2013, 11:28
Tu fais un tableau de variations.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 16 Déc 2013, 12:38
par nodjim » 16 Déc 2013, 12:38
La dérivée seconde ne te sert à rien pour ce problème.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 16 Déc 2013, 15:27
par Dante0 » 16 Déc 2013, 15:27
Sylviel a écrit:Tu fais un tableau de variations.
Ca fait 2 ans que j'en ai pas fait ^^
Je dois étudier le signe de la dérivée première exact ?
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 16 Déc 2013, 21:44
par Dante0 » 16 Déc 2013, 21:44
J'arrive pas à trouver cette valeur... :/
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Déc 2013, 09:03
par Sylviel » 17 Déc 2013, 09:03
Tu peux être plus synthétique qu'un tableau complet, mais oui, l'idée c'est d'étudier les variations, donc de calculer le signe de la dérivée pour affirmer ce que tu veux.
Sinon pour une parabole tu peux directement dire que "la parabole est orienté vers le haut" (coefficient en k² positif), donc le minimum sur un segment sera le plus prêt du sommet de la parabole (que tu as recalculé en cherchant le point où la dérivée s'annule). C'est sans doute dans un cours que tu as vu, et ça "se voit" sur n'importe quel schéma de parabole. La preuve se fait très simplement (et c'est ma première indication :zen: )
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 17 Déc 2013, 11:21
par Dante0 » 17 Déc 2013, 11:21
La fonction est décroissante sur -oo,1 et croissante sur 1,+oo
Mais je ne vois pas comment prouver que la fonction B admet un mimum pour K = 0,316 ? :hum:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Déc 2013, 11:29
par Sylviel » 17 Déc 2013, 11:29
Et bien tu t'impose que k<0.316
donc pour tout k' < 0.316
f(k') ... f(0.316)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 17 Déc 2013, 13:33
par Carpate » 17 Déc 2013, 13:33
Pas besoin d'un marteau-pilon pour écraser une mouche :
=(K-1)^2)
 \geq 0)
sur R, donc minimum en 0 pour
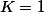
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 17 Déc 2013, 15:22
par Dante0 » 17 Déc 2013, 15:22
Sylviel a écrit:Et bien tu t'impose que k<0.316
donc pour tout k' < 0.316
f(k') ... f(0.316)
J'ai peur de ne pas te suivre. :triste:
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Déc 2013, 16:38
par Sylviel » 17 Déc 2013, 16:38
Ben c'est la définition même de décroissant !
Tu fais ton tableau, tu vois la flèche qui descend sur ]-OO,1], donc plus k est grand plus f(k) est petit (tant que tu restes sur cet intervalle). Du coup le minimum est forcément atteint au point le "à droite", donc en 0.316 car tu as comme contrainte que k soit plus petit que 0.316.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Dante0
- Membre Irrationnel
- Messages: 1243
- Enregistré le: 15 Nov 2010, 21:20
-
 par Dante0 » 17 Déc 2013, 18:00
par Dante0 » 17 Déc 2013, 18:00
Sylviel a écrit:Ben c'est la définition même de décroissant !
Tu fais ton tableau, tu vois la flèche qui descend sur ]-OO,1], donc plus k est grand plus f(k) est petit (tant que tu restes sur cet intervalle). Du coup le minimum est forcément atteint au point le "à droite", donc en 0.316 car tu as comme contrainte que k soit plus petit que 0.316.
Je vois merci ! :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités