Trouver l'erreur.

[Jack the ripper]

Salut à tous. Voici l'exercice sur lequel je bloque, il faut trouver l'erreur ( erreur de raisonnement ).

Soit n un entier naturel

Alors : (n+1)² = n²+2n+1
Donc : (n+1)²-(2n+1) = n²
Donc : (n+1)²-(2n+1)-n(2n+1) = n²-n(2n+1)
Donc : (n+1)²-(n+1)(2n+1) = n²-n(2n+1)
Donc : (n+1)²-(n+1)(2n+1)+1/4(2n+1)² = n²-n(2n+1)+1/4(2n+1)²
Donc : [(n+1)-1/2(2n+1)]² = [n-1/2(2n+1)]²
Donc : (n+1)-1/2(2n+1) = n-1/2(2n+1)
Donc : n+1-n-1/2 = n-n-1/2
Donc : n+1 = n

Voilà quelqu'un pourrait me mettre sur la piste si possible? J'ai quand même réfléchis sur la question mais il faut avouer que ça n'a pas porté ses fruits et je suis toujours dans la m..ouise. Merci d'avance :we:

[Monsieur23]

Bonjour.

Le problème se situe ici :

Donc : [(n+1)-1/2(2n+1)]² = [n-1/2(2n+1)]²
Donc : (n+1)-1/2(2n+1) = n-1/2(2n+1)

À toi de trouver pourquoi !

[titine]

Comment passe t on de la ligne 6 à la ligne 7 ...

[Jack the ripper]

D'accord, merci à vous 2.

Donc je réponds simplement en disant où est l'erreur et en justifiant par
a² = b² différents de a =b ?

[Monsieur23]

Il ne faut pas oublier que .

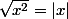
Ici, le terme de droite est négatif.

[oscar]

Bonjour
A gauche -> (n+1)² -(n+1)(2n+1) + 1/4 ( 2n+1)

A droite-> n² - n(2n+1) + 1/4 ( 2n+1) ² ( au carré...)( pas à gauche !!!

[Jack the ripper]

:cry: J'ai oublié le ² à l'étape n°5 en effet ( dans la fin du membre de gauche )

Mais vos réponses ne me donnent toujours pas le déclic :hum:

[Monsieur23]

Pour un exemple plus flagrant :

En faisant ce que tu dis, on a :

(-2)² = 2²
Donc 2=-2.

Tu comprends ?

[Jack the ripper]

Oui évidemment, mais l'appliquer à ce problème ...

Comment expliquer l'erreur en fait je ne comprends pas vor le principe


Edit : ah ok, mais donc en disant a² = b² diff de a=b c'est faux alors? :hum:

[Monsieur23]

[(n+1)-1/2(2n+1)]² = [n-1/2(2n+1)]²

Là, il se trouve que n-1/2(2n+1) est négatif ( et même égal à -1/2 si on développe ).

Donc en passant à la racine ( l'autre côté est positif ), on doit avoir :

[(n+1)-1/2(2n+1)] = - [n-1/2(2n+1)]

[Fanatic]

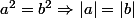
c'est tout. A toi ensuite d'étudier les cas possibles...

Oui évidemment, mais l'appliquer à ce problème ...

Comment expliquer l'erreur en fait je ne comprends pas vor le principe


Edit : ah ok, mais donc en disant a² = b² diff de a=b c'est faux alors? :hum:

[Jack the ripper]

C'est bon merci de m'avoir aidé :)