Trinôme et trigonométrie

[Laurette971]

Voilà ! J'ai un DM de maths de trois exos à faire pour la semaine prochaine et j'ai voulu m'y prendre à l'avance. J'ai réussi le premier exercice sans trop de problèmes mais je bloque un peu pour le deuxième, en particulier pour la questions 2.
Voici l'énoncé :


1) Résoudre dans R l'équation : 2x² - 3x + 1 = 0

;) = b² - 4ac
;) = (-3)² - 4x2x1
;) = 9-8
;) = 1>0 donc 2 solutions

x1 = (-b + ;);)) / 2a = 1
x2 = (-b - ;);)) / 2a = 1/2

2) En déduire les solutions dans R de l'équation : 2cos²(4t) - 3cos(4t) + 1 = 0
(commencer par poser x = cos(4t) )

Je reconnais parfaitement le trinôme précédant. J'en déduirais donc que ce sont les même solutions mais j'hésite.
J'aimerais donc que l'on m'éclaire.

Merci d'avance ! :help:

[Dinozzo13]

Salut !

Voilà ! J'ai un DM de maths de trois exos à faire pour la semaine prochaine et j'ai voulu m'y prendre à l'avance. J'ai réussi le premier exercice sans trop de problèmes mais je bloque un peu pour le deuxième, en particulier pour la questions 2.
Voici l'énoncé :


1) Résoudre dans R l'équation : 2x² - 3x + 1 = 0

= b² - 4ac
= (-3)² - 4x2x1
= 9-8
= 1>0 donc 2 solutions

x1 = (-b + ;)) / 2a = 1
x2 = (-b - ;)) / 2a = 1/2

2) En déduire les solutions dans R de l'équation : 2cos²(4t) - 3cos(4t) + 1 = 0
(commencer par poser x = cos(4t) )

Je reconnais parfaitement le trinôme précédant. J'en déduirais donc que ce sont les même solutions mais j'hésite.
J'aimerais donc que l'on m'éclaire.

Merci d'avance ! :help:

Evidement, ce n'est pas anodin :++:

En posant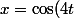 Les solutions sont ou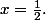
Donc les solutions dans R de 2cos²(4t) - 3cos(4t) + 1 = 0, sont solutions de et

[Laurette971]

Merci beaucoup ! Faut-il par contre que je précise cos(4t)1 et cos(4t)2 comme on fait pour x1 et x2 ?

[Dinozzo13]

Attention :

Tu dois résoudre séparément les équations et .
Si on note respectivement et l'ensemble des solutions de ces deux équations alors l'ensemble des solutions de l'équation est .

:+++:

[Laurette971]

Si j'ai bien compris, je dois remplacer cos(4t) dans l'équation selon sa valeur. En faisant ça j'obtiens comme prévu 0 dans chaque cas. Mais j'avoue ne pas avoir compris le reste de ta réponse. =$

[Dinozzo13]

Ben x=1 ou x=1/2 donc cos(4t)=1 ou cos(4t)=1/2 donc t=... ou t=... .
Donc S=...

[Joker62]

Bonsoir,

Tu as résolu 2x^2 - 3x + 1 = 0
Tu as trouvé deux solutions : x_1 = 1/2 et x_2 = 1

Si maintenant, on te demande de résoudre :

2*Patate^2 - 3*Patate + 1 = 0 tu es sûre que Patate vaut soit 1/2 soit 1.

Tu dois donc écrire : Patate = 1/2 ou Patate = 1.

Ici Patate = cos(4t)
Ainsi

Les solutions de 2*cos(4t)^2 - 3*cos(4t) + 1 = 0 sont tous les t tels que
cos(4t) = 1/2 ou cos(4t) = 1

Il faut donc résoudre deux équations trigonométriques pour trouver les t

[Laurette971]

Salut Joker62 ! C'est super sympa d'apporter ton aide ! Vous devez pensez que je suis complètement nulle mais niveau maths ... autant y'a des trucs que je comprends super rapidement mais d'autres où c'est carrément le contraire. Et cette fois c'est la trigonométrie.
Dans l'exercice en question je crois que c'est le 4t qui me bloque. :/

[Joker62]

On a le théorème suivant :

cos(x) = cos(a) <=> x = a + 2*k*;) ou x = -a + 2*l*;)

Donc comme 1/2 = cos(;)/3), on a :

cos(4t) = cos(0) <=> 4t = ;)/3 + 2*k*;) ou 4t = -;)/3 + 2*l*;)

Il faut isoler le t comme dans les équations classiques.

[Laurette971]

Pourquoi cos(0) ?! (Désolée d'être aussi chiante =$ )

[Laurette971]

Ah ! Ne serait-ce pas parce que cos(0) = 1 ?!

[Joker62]

Parce que je me suis trompé.

Je voulais mettre cos(;)/3) excuse moi.

[Dinozzo13]

On a le théorème suivant :

cos(x) = cos(a) x = a + 2*k*;) ou x = -a + 2*l*;)

Donc comme 1/2 = cos(;)/3), on a :

cos(4t) = cos(0) 4t = /3 + 2*k*;) ou 4t = -;)/3 + 2*l*;)

Il faut isoler le t comme dans les équations classiques.

Au temps pour moi, je croyais que Laurette971 l'avait compris :++:

[Laurette971]

Tentative de réponse :

cos(4t) = cos(;)/3) <=> 4t = ;)/3 + 2k;) <=> t = ;)/12 + (1/2) 2k;)
ou 4t = -;)/3 + 2k;) <=> t = -;)/12 + (1/2)2k;)

cos(4t) = cos(0) <=> 4t = 2k;) <=> t = (1/2)2k;)

[Dinozzo13]

Tentative de réponse :

cos(4t) = cos(;)/3) 4t = /3 + 2k;) t = /12 + (1/2) 2k;)
ou 4t = -;)/3 + 2k;) t = -;)/12 + (1/2)2k;)

cos(4t) = cos(0) 4t = 2k;) t = (1/2)2k;)

Nam, pas d'accord :

ou

et :

[Laurette971]

Ouii ! Pardon c'est l'habitude de mettre 2k;) ! Faute d'inattention !
Sinon est-ce correct ?!

[Laurette971]

J'aimerais une dernière fois faire appel à l'un de vous concernant la rédaction finale de la question 2 de mon exercice :
PS : la totalité des calculs figurera sur ma copie

Donc:

En posant x=cos(4t) on obtient x=1 ou x=1/2
Par conséquent, les solutions de 2cos²(4t)-3cos(4t)+1=0 dans R sont cos(4t)=1 ou cos(4t)=1/2.

On sait que 1/2=cos(;)/3) et que 1=cos(0) donc :

- cos(4t) = cos(;)/3) <=> 4t = ;)/3 + 2k;) <=> t = ;)/12 + 1/2k;)
ou 4t = -;)/3 + 2k;) <=> t = -;)/12 + 1/2k;)

- cos(4t) = cos(0) <=> 4t = 2k;) <=> t = 1/2k;)

Donc S= {;)/12 + 1/2k;) ; -;)/12 + 1/2k;) ; 1/2k;)} dans R


Est-ce correct sinon quelles sont les modifications à apporter ?

[Laurette971]

Je te remercie énormément de ton aide Joker62. Elle m'a été très utile. Encore merci !