Trigonometrie

par **mohcine_math** » 07 Sep 2005, 12:37

salut à tout le monde
j ai un petit exercice que j ai pas encore arrivé à sa solution il m a semblé absure ,la raison pour laquelle je me suis adressé à vous

soit a,b et c trois points du cercle trigonometrique d abscisse curvilignes $\alpha$, $alpha$ + ${2\pi}\over 3$,$\alpha$ + ${4pi}\over 3$ respectivement, avec $\alpha$ de $\Re$

une petite remarque : moi j ai pas encore vu le cours,alors que la question presente peut etre facile, si c est le cas n hesitez quand meme pas de me poster la reponse .

par **Nicolas_75** » 07 Sep 2005, 12:40

Mais... quelle est la question ?

par **mohcine_math** » 07 Sep 2005, 12:44

montrer que abc est un triangle equilatère.

par **mohcine_math** » 08 Sep 2005, 12:04

vous voulez pas repondre ?

par **S@m** » 08 Sep 2005, 13:19

Faudrait que tu reedite pour qu'on comprenne mieux et pour qu'on puisse repondre a ta question... :++:Tu sais comment utiliser les balises TEX? si non tu peux aller jeter un coup d'oeil ici http://www.maths-forum.com/showthread.php?t=3414

par **mohcine_math** » 08 Sep 2005, 14:06

salut à tout le monde
j ai un petit exercice que j ai pas encore arrivé à sa solution il m a semblé absure ,la raison pour laquelle je me suis adressé à vous

soit a,b et c trois points du cercle trigonometrique d abscisse curvilignes :

,

+

,

+

respectivement, avec

de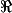

.
montrer que abc est un triangle equilatère.

une petite remarque : moi j ai pas encore vu le cours,alors que la question presente peut etre facile, si c est le cas n hesitez quand meme pas de me poster la reponse.

par **Nicolas_75** » 08 Sep 2005, 14:51

Chacun des triangles OAB, OBC et OCA :
- a pour même angle en O 2pi/3 (relation entre angle et abscisses curviligne)
- est isocèle avec la même longueur pour les 2 côtés de même longueur.
Donc ces 3 triangles sont superposables.
Donc AB=BC=CA et ABC est équilatéral

Trigonometrie

trigonometrie

Qui est en ligne