Salut . J ai un souci s il vous plaît .
Exercice.
1) x et y sont des réels de l intervalle ,[π/2;π] et cos x =3/5 et cosy=1/3. Calculer cos (2x-y).
2) on considère le réel x E ]π/2;π[ et cos(π/2 -x). =2/3 . Calculer cosx ;cos2x; sin2x; et tan2x
Merci pour l attention
Trigonometrie
9 messages
- Page 1 sur 1
Re: Trigonometrie
Bonjour,
Dans ton cas, le cos x= - 3/5 et cos y = - 1/3
C'est d'après intervalle que tu viens de donner.
Dessine le cercle trigonométrique et regarde le signe des cosinus dans ton intervalle..
Dans ton cas, le cos x= - 3/5 et cos y = - 1/3
C'est d'après intervalle que tu viens de donner.
Dessine le cercle trigonométrique et regarde le signe des cosinus dans ton intervalle..
Re: Trigonometrie
Bonjour AMARI,
pourquoi donner la réponse, alors que j'attendais plutôt celle de Iranelle
pourquoi donner la réponse, alors que j'attendais plutôt celle de Iranelle
Re: Trigonometrie
Bonjour Pisigma,
Ce n'est qu'une orientation, mais le reste est plus important à trouver.
Merci
Ce n'est qu'une orientation, mais le reste est plus important à trouver.
Merci
Re: Trigonometrie
Bonjour,
1)
On peut trouver x par la fonction arc cos
Idem pour y remplacons x et y par des arc cos et calculons le cos demande.
2)
On peut trouver x grâce à arc cos et le remplacer pour trouver les cos sin tan demande.
1)
On peut trouver x par la fonction arc cos
Idem pour y remplacons x et y par des arc cos et calculons le cos demande.
2)
On peut trouver x grâce à arc cos et le remplacer pour trouver les cos sin tan demande.
Re: Trigonometrie
Bonjour mathou13
est-ce la méthode attendue?
ne connaissant pas bien les pgm du Lycée, tu as peut-être raison
mathou13 a écrit:Bonjour,
1)
On peut trouver x par la fonction arc cos
Idem pour y remplacons x et y par des arc cos et calculons le cos demande.
2)
On peut trouver x grâce à arc cos et le remplacer pour trouver les cos sin tan demande.
est-ce la méthode attendue?
ne connaissant pas bien les pgm du Lycée, tu as peut-être raison
Re: Trigonometrie
bonsoir,
question 1:
les deux cosinus sont négatifs et les deux sinus sont positifs.
de l'identité
+sin^2(x)=1)
on tire
=\sqrt{1-cos^2(x)})
ce qui permet de calculer les deux sinus.
soient a et b deux réels
développe cos(a-b).
de plus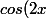=2 cos^2(x)-1) et
et =2 sin(x) cos(x)) pour tout x réel.
pour tout x réel.
question 1:
les deux cosinus sont négatifs et les deux sinus sont positifs.
de l'identité
on tire
ce qui permet de calculer les deux sinus.
soient a et b deux réels
développe cos(a-b).
de plus
Re: Trigonometrie
Bonsoir,
question 1:
cos x = -3/5, cos y =-1/3
on calcule les sinus (positifs)

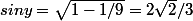
on calcule les lignes trigonométriques de 2x:
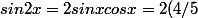(-3/5)=-24/25)
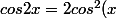-1=2(9/25)-1=-7/25)
=cos 2x \, cos y + sin 2x \, sin y)
=(-7/25)(-1/3)+(-24/25)(2 \sqrt{2})/3)=(1/75)(7-48 \sqrt{2}) \sim -0,812)
question 1:
cos x = -3/5, cos y =-1/3
on calcule les sinus (positifs)
on calcule les lignes trigonométriques de 2x:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
