Trigonometrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bcka270
- Messages: 9
- Enregistré le: 23 Déc 2021, 00:27
-
 par Bcka270 » 23 Déc 2021, 00:42
par Bcka270 » 23 Déc 2021, 00:42
Bonjour à tous ,
j'ai un exercice mais je ne sais pas ce qu'il faut faire exactement.
Exprimer cos(x+y) et sin(x+y) en fonction de sin(x), cos(x),sin(y) et cos(y)
Une aide ? Merci d'avance

-
mathelot
 par mathelot » 23 Déc 2021, 01:01
par mathelot » 23 Déc 2021, 01:01
Bonsoir,
à partir du produit scalaire
Soit le cercle trigo (centre O origine, rayon r=1) et deux points A et B du cercle.
Avec les coordonnées des deux vecteurs dans une base orthonormée:
il existe
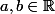
tels que
;sin(a)))
et
;sin(b)))
on exprime le produit scalaire de
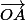
par
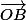
de deux manières:
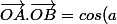cos(b)+sin(a)sin(b)=||\vec{OA}||||\vec{OB}|| cos(b-a)=cos(b-a))
d'où
=cos(a)cos(b)+sin(a)sin(b))
en changeant

en

, il vient:
=cos(a)cos(b)-sin(a)sin(b))
soit
=cos(x)cos(y)-sin(x)sin(y))
on sait d'autre part que
=cos(\frac{\pi}{2}-x))
=sin(\frac{\pi}{2}-x))
d'où
=cos(\frac{\pi}{2}-x-y))
=cos((\frac{\pi}{2}-x)-y))
=cos(\frac{\pi}{2}-x)cos(y) +sin(\frac{\pi}{2}-x)sin(y))
=sin(x)cos(y)+cos(x)sin(y))
Modifié en dernier par mathelot le 23 Déc 2021, 01:15, modifié 1 fois.
-
mathelot
 par mathelot » 23 Déc 2021, 01:12
par mathelot » 23 Déc 2021, 01:12
-
Bcka270
- Messages: 9
- Enregistré le: 23 Déc 2021, 00:27
-
 par Bcka270 » 23 Déc 2021, 13:31
par Bcka270 » 23 Déc 2021, 13:31
Un très grand merci !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Déc 2021, 15:51
par Ben314 » 23 Déc 2021, 15:51
Salut,
On peut aussi voir le résultat avec de la simple géométrie : si A:(cos(a),sin(a)), B:(cos(a+b),sin(a+b)) et que C est le projeté orthogonal de B sur la droite (OA), le fait que l'angle entre le vecteur OA et le vecteur OB soit b signifie que (en vecteurs)
OB=OC+CB=cos (b)OA+sin (b)OA'
Où A':(cos(a+pi/2),sin(a+pi/2))=(-sin(a),cos(a))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités