Trigonométrie

[LPPV]

Bonjour ,

Voici ma question :

Sois le triangle ABC représenté ci-contre
Dance ce triangle , le théoreme d'Al-Kashi s'exprime :

a² = b²+ c² - 2xBxCxCOS A

1 - Sois AC : 75 mm. AB:58mm et A : 60° . Calculer BC ( arrondir a 0.1 mm )

2 -Soit un triangle quelconque A'B'C tel que A'C = 85 mm. B'C = 102 mm et C = 42°( arrondir a 0.1 mm )


ps : J'ai beaucoup de difficulté en math
et pour la figure je ne sais pas comment la faire parvenir

[Titahn]

Bonjour ,

Voici ma question :

Sois le triangle ABC représenté ci-contre
Dance ce triangle , le théoreme d'Al-Kashi s'exprime :

a² = b²+ c² - 2xBxCxCOS A

1 - Sois AC : 75 mm. AB:58mm et A : 60° . Calculer BC ( arrondir a 0.1 mm )

2 -Soit un triangle quelconque A'B'C tel que A'C = 85 mm. B'C = 102 mm et C = 42°( arrondir a 0.1 mm )


ps : J'ai beaucoup de difficulté en math
et pour la figure je ne sais pas comment la faire parvenir

Salut, ne t'en fais pas pour tes difficultés, on est là pour t'aider =).

Pour l'image, tu peux l'héberger ici : http://imageshack.us/ et ensuite nous faire parvenir un lien (ou directement l'intégrer dans ton message avec la balise d'image :

Et j'ai l'impression que ta seconde question manque de... Question ^^.

[chan79]

Bonjour
BC²=AB²+AC²-2.AB.AC.cos A
Tu as juste à remplacer

[ampholyte]

Bonjour,

Il suffit de faire correspondre les données de l'énoncé à la formule du théorème d'Al-Kashi.

Ce n'est pas très compliqué :

1) AB correspond à c
AC correspond à b
BC correspond à a

Donc ...

2) Même principe

A'B' = c
A'C = b
B'C = a

[LPPV]

Salut, ne t'en fais pas pour tes difficultés, on est là pour t'aider =).

Pour l'image, tu peux l'héberger ici : http://imageshack.us/ et ensuite nous faire parvenir un lien (ou directement l'intégrer dans ton message avec la balise d'image :

Et j'ai l'impression que ta seconde question manque de... Question ^^.

Merci beaucoup :!)

Pour la deuxieme question , je trouve aussi mais c'est pourtant mon professeur qui me la donner

[Titahn]

Merci beaucoup :!)

Pour la deuxieme question , je trouve aussi mais c'est pourtant mon professeur qui me la donner

Pour la seconde question, il faut probablement calculer A'B' ^^

[LPPV]

Bonjour
BC²=AB²+AC²-2.AB.AC.cos A
Tu as juste à remplacer

Pour la question n°1 ?

[LPPV]

Bonjour,

Il suffit de faire correspondre les données de l'énoncé à la formule du théorème d'Al-Kashi.

Ce n'est pas très compliqué :

1) AB correspond à c
AC correspond à b
BC correspond à a

Donc ...

2) Même principe

A'B' = c
A'C = b
B'C = a

Merci beaucoup !!

[LPPV]

Bonjour
BC²=AB²+AC²-2.AB.AC.cos A
Tu as juste à remplacer

Merci beaucoup

[chan79]

Merci beaucoup

tu trouves quoi, finalement ?

[Titahn]

Puisque tu es nouveau dans le coin, sache qu'il est préférable d'éviter de poster 2 ou 3 fois à la suite, si tu peux éviter. Mets tout dans le même message, ce sera mieux ;)

[LPPV]

tu trouves quoi, finalement ?

Je n'ai pas tres bien compris , si je fait BC²=AB²+AC²-2.AB.AC.cos A donc chaque valeur qui correspond je multiplie par 2 puisque c'est au ² ?

[ampholyte]

Oula attention de ne pas confondre 2BC = BC + BC et BC² = BC * BC

[Titahn]

Je n'ai pas tres bien compris , si je fait BC²=AB²+AC²-2.AB.AC.cos A donc chaque valeur qui correspond je multiplie par 2 puisque c'est au ² ?

Non !

Pour rappel : x²=x*x
Donc 5²=5*5=25

Ici faut donc que tu multiplies chaque valeur par elle-même.

[LPPV]

Oula attention de ne pas confondre 2BC = BC + BC et BC² = BC * BC

Ah oui , donc pour cette situation c'est plutôt BC*BC ?

[ampholyte]

Non, c'est bien BC².

Pour obtenir BC il faudra prendre la racine carrée :

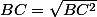
donc en calculant BC² tu trouveras facilement BC

[LPPV]

Non !

Pour rappel : x²=x*x
Donc 5²=5*5=25

Ici faut donc que tu multiplies chaque valeur par elle-même.

Donc BC²= 58X58 + 75X75 - 2x58x75x60

Le resultat me parais bizard quand je calcule tout

[ampholyte]

peut-être parce que tu oublies que c'est cos(60°) ?

Ensuite il faut prendre la racine de BC² pour obtenir la vrai valeur.

Qu'obtiens-tu ? (perso je trouve pour BC entre 35mm et 40mm pour ne pas te donner le résultat précis =))

[LPPV]

peut-être parce que tu oublies que c'est cos(60°) ?

Ensuite il faut prendre la racine de BC² pour obtenir la vrai valeur.

Qu'obtiens-tu ? (perso je trouve pour BC entre 35mm et 40mm pour ne pas te donner le résultat précis =))

Ba déjà pour AB² si je fais 58X58 sa me fait 3364 et pour AC² je fais 75X75 sa me fait 5625

Je ne comprend pas trop ..

[ampholyte]

C'est le bon résultat donc qu'est-ce que tu comprends pas ?