Trigonometrie

[vincepi]

Bonjour,
je navigue en eaux troubles avec mon equation:
merci à ceux qui pourront m'aider voilà ce que j'ai fais:

[chan79]

salut
Commence par le domaine de définition

[Shew]

Bonjour,
je navigue en eaux troubles avec mon equation:
merci à ceux qui pourront m'aider voilà ce que j'ai fais:

= ????

[vincepi]

= ????

ici

c'est ca???

[Shew]

ici

c'est ca???

Enfait cette partie était bonne c'est juste que je n'avais pas compris la syntaxe latex .

Par contre je ne comprends pas comment vous passez de ça



à ça

[vincepi]

Enfait cette partie était bonne c'est juste que je n'avais pas compris la syntaxe latex .

Par contre je ne comprends pas comment vous passez de ça



à ça

non en fait j'arrive à
??

[Shew]

non en fait j'arrive à
??

Si je ne m'abuse vous pouvez faire disparaître le signe négatif

[chan79]

non en fait j'arrive à
??

pour k=0, ça va
pour k=1, ça ne va pas

[Shew]

pour k=0, ça va
pour k=1, ça ne va pas

Oui en effet seul un cadran du cercle est solution

[chan79]

Oui en effet seul un cadran du cercle est solution

11pi/12 est solution

[Shew]

11pi/12 est solution

Ok, la je seche parce qu'en restant dans le contexte de l'equation je ne l'aurais pas trouvé (à moins de faire toutes les valeurs du cercle )

[EDIT] Ca y'est je saisi , désolé Chan je n'avais pas vu le truc sur le moment . Donc la solution trouvée au départ était presque bonne juste à régler un problème de signe et à terminer la simplification

[Aredhell]

pour k=0, ça va
pour k=1, ça ne va pas

Oui car :

[Shew]

Oui car :

Oui , en même temps je ne suis pas certain (je m'avance peut être) que vincepi comprenne cette approche .

[chan79]

Salut
Une idée de rédaction
Il faut que soit différent de
et que soit différent de
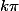
ces deux conditions se résument à x différent de (points rouges de la figure jointe).
Ensuite l'équation équivaut à:


donc


mais il faut exclure certaines valeurs (points rouges) pour ne garder que les points bleus


solutions modulo

[Shew]

Salut
Une idée de rédaction
Il faut que soit différent de
et que soit différent de
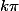
ces deux conditions se résument à x différent de (points rouges de la figure jointe).
Ensuite l'équation équivaut à:


donc


mais il faut exclure certaines valeurs (points rouges) pour ne garder que les points bleus


solutions modulo

Et pour , comment l'inclure ?

[chan79]

Et pour , comment l'inclure ?

Finalement, les solutions (points bleus) sont





qui donne les mêmes solutions que

[Shew]

Finalement, les solutions (points bleus) sont





qui donne les mêmes solutions que

Je comprends . Merci d'avoir pris le temps de m'expliquer :lol3:

[Black Jack]

tg(x+Pi/3) + cotg(Pi/2 - 3x) = 0

N'existe pas si x + Pi/3 = Pi/2 + k'.Pi ou si Pi/2 - 3x = k'.Pi

---> valeurs interdites: x = Pi/6 + k'.Pi et x = Pi/6 + k'.Pi/3
Qui se réduisent en : valeurs interdites: x = Pi/6 + k'.Pi/3 (1)

tg(x + Pi/3) + cotg(Pi/2 - (Pi/2 - 3x)) = 0
tg(x + Pi/3) + tg(3x) = 0
tg(x + Pi/3) = tg(-3x)

x + Pi/3 = -3x + k.Pi (car tg est Pi périodique)
4x = -Pi/3 + k.Pi
x = -Pi/12 + k.Pi/4
Mais il faut tenir compte de (1) ...

Donc : -Pi/12 + k.Pi/4 = Pi/6 + k'.Pi/3 est interdit
-1/12 + k/4 = 1/6 + k'/3
-1 + 3k = 2 + 4k'
3k = 3 + 4k'
k = 1 + 4k'/3
avec k et k' entiers ----> k = 1 + 4p est interdit (avec p dans Z)

valeurs permises pour k :
a) 4K
b) 2 + 4K
c) 3 + 4K
(Avec K dans Z)

Les solutions sont donc :

a) x = -Pi/12 + (4K).Pi/4
b) x = -Pi/12 + (2+4K).Pi/4
c) x = -Pi/12 + (3+4K).Pi/4

Soit donc :
a) x = -Pi/12 + K.Pi
b) x = 5Pi/12 + K.Pi
c) x = 2Pi/3 + K.Pi
Avec K dans Z.

:zen:

[Shew]

Petite question , pour pourquoi ne pas commencer directement par et ainsi éliminer le signe négatif , puisque se trouve dans la solution ?

[Black Jack]

Petite question , pour pourquoi ne pas commencer directement par et ainsi éliminer le signe négatif , puisque se trouve dans la solution ?

C'est chou vert et vert chou... à condition de ne pas oublier le +k.Pi

:zen: