Trigonométrie exercice long
12 messages
- Page 1 sur 1
Trigonométrie exercice long
Bonjour , j'envoi ce message pour savoir si quelqu'un pouvait corrigé les deux premières question(ou même la 1ere) svp?
https://ibb.co/P9NLJkR
https://ibb.co/P9NLJkR
Re: Trigonométrie exercice long
Re,
il faut bien que les résultats demandés se déduisent d'hypothèses. Quelle théorie va-t-on supposer connue ? Quels résultats de classe de 1ère va-t-on utiliser ?
il faut bien que les résultats demandés se déduisent d'hypothèses. Quelle théorie va-t-on supposer connue ? Quels résultats de classe de 1ère va-t-on utiliser ?
Re: Trigonométrie exercice long
Euh je vais replonger dans mes cours de 1ère,
par contre j'ai schématisé tout ça, et j'appel M' le projeté orthogonal du point M sur l'axe des abscisses.
Ainsi OMM' est un triangle rectangle en M'.
Nous savons que le cercle est le cercle de centre O(0,0) car x²+y²=1. (cercle de rayon 1).
Nous pouvons en déduire (grace au théorème de Pythagore) que cos²théta+sin²théta=1.
Cela montre que les coordonnées du point M sont bien M(cos théta,sin théta).
Par la suite le coefficient directeur de la droite sera a= sin théta/cos théta.
Et la droite sera vertical si théta = pi/2 (je pense)
par contre j'ai schématisé tout ça, et j'appel M' le projeté orthogonal du point M sur l'axe des abscisses.
Ainsi OMM' est un triangle rectangle en M'.
Nous savons que le cercle est le cercle de centre O(0,0) car x²+y²=1. (cercle de rayon 1).
Nous pouvons en déduire (grace au théorème de Pythagore) que cos²théta+sin²théta=1.
Cela montre que les coordonnées du point M sont bien M(cos théta,sin théta).
Par la suite le coefficient directeur de la droite sera a= sin théta/cos théta.
Et la droite sera vertical si théta = pi/2 (je pense)
Re: Trigonométrie exercice long
Bonsoir,
on va utiliser les propriétés du produit scalaire, noté "."
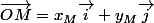
La base étant orthonormée, on obtient
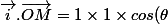=x_M)
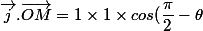=\sin(\theta)=y_M)
on va utiliser les propriétés du produit scalaire, noté "."
La base étant orthonormée, on obtient
Re: Trigonométrie exercice long
Ah bin oui !
Ah j'ai été me compliqué la vie avec mon schéma et le théorème de Pythagore
Ah j'ai été me compliqué la vie avec mon schéma et le théorème de Pythagore
Re: Trigonométrie exercice long
mathelot a écrit:Question c Que faire ?
Je sens que c'est pas une question difficile
Si c'était deux équation de fonctions affine , constante ou linéaire, j'aurai dis qu'il faudrai trouver les coordonnées du point d'intersection on peut utiliser l'équation des deux droites et résoudre le système :
x=1
y = sin théta/cos théta
je vais me pencher sur un autre piste de réflexion ce soir, ce chemin est sans issue
Re: Trigonométrie exercice long
re,
question 1,c
La droite (D) est parallèle à (MM'). Les points OM'M et OIP forment une configuration de Thalès.
on a:
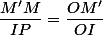
}{IP}=\dfrac{\cos(\theta)}{1})
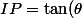)
P a pour coordonnées))
question 1,c
La droite (D) est parallèle à (MM'). Les points OM'M et OIP forment une configuration de Thalès.
on a:
P a pour coordonnées
Re: Trigonométrie exercice long
Question 2.c
Soit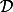 et
et ) deux domaines plan mesurables. (on dispose d'une formule ou d'un algorithme pour calculer leurs aires).
deux domaines plan mesurables. (on dispose d'une formule ou d'un algorithme pour calculer leurs aires).
Si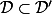 alors Aire(
alors Aire(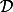 )
)  Aire(
Aire(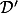 )
)
Soit
Si
Re: Trigonométrie exercice long
Je vous remercie infiniment, mon ordinateur était en panne mais je referai cet exo
Re: Trigonométrie exercice long
re-bonjour,
2.a l'aire du triangle OIM vaut 1/2(base x hauteur)
Aire=\dfrac{1 \times \sin(\theta)}{2}=(1/2) \sin(\theta))
2.b l'aire du triangle OIM vaut 1/2(base x hauteur)
Aire=\dfrac{1 \times \tan(\theta)}{2}=(1/2) \tan(\theta))
Aire du secteur angulaire (OIM) : \theta)
2.c
On a les inclusions d'ensembles:
 \subset OIP)
 sin(\theta) \leq (1/2) \theta \leq (1/2) \tan(\theta))
pour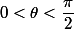
} \leq \dfrac{1}{\cos(\theta)})
Par le théorème des gendarmes
}=1)
pour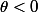
}=\dfrac{-\theta}{\sin(-\theta)})
}=1)
et donc
}=1)
Question 3
,\sin(\theta)))
,\sin(\theta')))
d'où
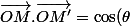 cos(\theta')+\sin(\theta) sin(\theta'))
On a deux expressions du produit scalaire:
)
=\cos(\theta) cos(\theta')+\sin(\theta) sin(\theta'))
2.a l'aire du triangle OIM vaut 1/2(base x hauteur)
Aire
2.b l'aire du triangle OIM vaut 1/2(base x hauteur)
Aire
Aire du secteur angulaire (OIM) :
2.c
On a les inclusions d'ensembles:
pour
Par le théorème des gendarmes
pour
et donc
Question 3
d'où
On a deux expressions du produit scalaire:
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
