Cos x - sin x =
Trigonométrie,1ère S
25 messages
- Page 1 sur 2 - 1, 2
Trigonométrie,1ère S
S'il vous plait comment determiner cos x et sin x en sachant que :
Cos x - sin x =
Cos x - sin x =
Perso, j'aurais fait comme tototo, voir même commencé par tracer le cercle trigo et la droite d'équation x-y=1/2 sur une feuille histoire de dégrossir le problème...
Sinon, pour simplifier=a\cos(t)+b\sin(t)) , une méthode classique, c'est d'écrire les coordonnées polaires du point (a,b), c'est à dire d'écrire
, une méthode classique, c'est d'écrire les coordonnées polaires du point (a,b), c'est à dire d'écrire 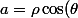) ;
; 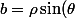) (donc
(donc 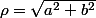 ) qui donne
) qui donne =\rho\cos(t-\theta)) (fréquemment utilisé en physique par exemple pour simplifier
(fréquemment utilisé en physique par exemple pour simplifier =\sum_{k=1}^n \rho_k\sin(t-t_k)) )
)
Sinon, pour simplifier
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Perso, j'aurais fait comme tototo, voir même commencé par tracer le cercle trigo et la droite d'équation x-y=1/2 sur une feuille histoire de dégrossir le problème...
Sinon, pour simplifier, une méthode classique, c'est d'écrire les coordonnées polaires du point (a,b), c'est à dire d'écrire
;
(donc
) qui donne
(fréquemment utilisé en physique par exemple pour simplifier
)
En 1eS, ils n'ont pas encore vu les formules d'addition du sin et du cos.
L'équation de tototo ne nous avance pas beaucoup ?
O.K. pour la première phrase, mais je comprend pas le sens ? a la fin de la deuxième : ils ne font plus les équations du second degré en première ?PSEUDA a écrit:En 1eS, ils n'ont pas encore vu les formules d'addition du sin et du cos.
L'équation de tototo ne nous avance pas beaucoup ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:O.K. pour la première phrase, mais je comprend pas le sens ? a la fin de la deuxième : ils ne font plus les équations du second degré en première ?
Ce n'est pas cela. Ils les font, mais la résolution de cette équation nous donne une solution en cos x = (1+V7)/4 (voir message de Mathelot), ce qui revient au même (cela ne nous avance pas plus) que sin (2x) = 3/4 ou cos (x+;)/4)=1/(2V2).
mathelot a écrit:1ère méthode
On pose (X,Y) les coordonnées cartésiennes du point M(cos(x),sin(x)).
Il vientsont solutions de
ou
[2ème méthode
De cos(a+b)=cos(a)cos(b)-sin(a)sin(b)
il vient:
ou
3ème méthode
On élève au carré l'équation, il vient:
ou
Oui, je n'ai pas vérifié tous les calculs (j'ai juste trouvé la solution 0,424...), et il est intéressant de voir que :
salut
variante:
on demande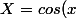) et
et 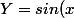) sachant que
sachant que 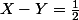
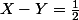

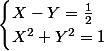
^2=1 \end{cases})
On résout l'équation du second degré qui se ramène à
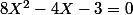
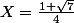 ou
ou 
on retranche 1/2 à X pour obtenir Y.
=\(\frac{1+\sqrt{7}}{4};\frac{-1+\sqrt{7}}{4}\))
ou
=\(\frac{1-\sqrt{7}}{4};\frac{-1-\sqrt{7}}{4}\))
Si on veut les x (ce n'est pas demandé)
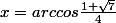 \ (modulo\ 2 \pi)) (0,424...modulo 2
(0,424...modulo 2 )
)
ou
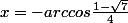 \ (modulo\ 2 \pi)) (-1,994... modulo 2
(-1,994... modulo 2 )
)
variante:
on demande
On résout l'équation du second degré qui se ramène à
on retranche 1/2 à X pour obtenir Y.
ou
Si on veut les x (ce n'est pas demandé)
ou
Modifié en dernier par chan79 le 13 Jan 2016, 15:53, modifié 7 fois.
chan79 a écrit:A noter que les équations:
cos(x)-sin(x)=1/2
et
sin(2x)=3/4
n'ont pas les mêmes ensembles de solutions.
(on ajoute des solutions en élevant la première au carré)
C'est sûr. L'approche du problème est entièrement différente selon que l'on cherche à résoudre l'équation en cos x et sin x, ou bien en x. J'ai lu l'énoncé trop vite.
Re:
mathelot a écrit:moi aussi, je n'avais pas tilté qu'il fallait calculer cos(x) et non pas x.
On est deux. Moralité : bien lire les énoncés....
 Re: Trigonométrie,1ère S
Re: Trigonométrie,1ère S
S'il vous plait vous n'avez aucune solution?
Et une donnée en plus dans l'exercice il est dit :
Calculer cos x et sin x sachant que :
Cos x - sin x = et que:
et que:
^2+(cos x - sin x )^2) = 2
= 2
Et une donnée en plus dans l'exercice il est dit :
Calculer cos x et sin x sachant que :
Cos x - sin x =
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
