Trigo seconde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 09 Mai 2010, 13:34
par nicolas202 » 09 Mai 2010, 13:34
Bonjour, pour demain je dois démontrer des formules trigonométriques en s'appuyant sur la relation fondamentale : sin2x + cos2 = 1 et de tanx = sinx/ cosx. Je bloque sur celle là : (1- tan^2) / ( 1+tan^2)
Je dois démontrer que c'est égal à : cos^2 / sin^2
* Ce sont les cosinus, sinus et tangente de alpha
Merci d'avance ! :we:
-
sylvainp
- Membre Relatif
- Messages: 383
- Enregistré le: 09 Fév 2007, 19:58
-
 par sylvainp » 09 Mai 2010, 14:02
par sylvainp » 09 Mai 2010, 14:02
salut t'es sûr de ton égalité?
tu peux remplacer tan par sin/cos et mettre sur le même dénominateur 1-sin/cos et1+sin/cos

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 09 Mai 2010, 14:06
par Ericovitchi » 09 Mai 2010, 14:06
tu vas avoir du mal car ça n'est pas égal à ce que tu dis.
Si tu pars de (1- tan^2) / ( 1+tan^2) que tu écris la tangente sin/cos, que tu réduis au même dénominateur, tu trouves cos²x-sin²x donc cos 2x et pas 1/tan²
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 09 Mai 2010, 14:07
par oscar » 09 Mai 2010, 14:07
( 1- tg ²x) / ( 1+tg²x)=
( 1 -sin²x)/cos ²x)( 1+ sin²x /cos ²x)=
(cos ²x -sin²x) /( cos²x +sin²x)=
cosx - sin²x=????
-
Sve@r
 par Sve@r » 09 Mai 2010, 14:08
par Sve@r » 09 Mai 2010, 14:08
nicolas202 a écrit:Bonjour, pour demain je dois démontrer des formules trigonométriques en s'appuyant sur la relation fondamentale : sin2x + cos2 = 1 et de tanx = sinx/ cosx. Je bloque sur celle là : (1- tan^2) / ( 1+tan^2)
Je dois démontrer que c'est égal à : cos^2 / sin^2
Désolé, t'as qu'à essayer avec un exemple concret car

n'est pas égal à

. Perso je dirais plutôt que c'est égal à cos² - sin² ...
-
nicolas202
- Membre Naturel
- Messages: 28
- Enregistré le: 15 Sep 2009, 15:59
-
 par nicolas202 » 09 Mai 2010, 17:36
par nicolas202 » 09 Mai 2010, 17:36
Merci beaucoup ! à tous ! J'avais bien trouvé la meme chose que vous , j'ai du en effet me tromper dans mon énoncé !
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 09 Mai 2010, 17:55
par Arnaud-29-31 » 09 Mai 2010, 17:55
Bonjour,
Ton truc me fait beaucoup penser au formules de l'angle moitié ...
T'es sur que tu ne dois pas démontrer que
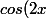 = \frac{1 - tan^2x}{1 + tan^2x})
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
