Triangles

par **TooLate** » 26 Fév 2015, 21:12

Bonjour à tous.
J'aurais besoin d'aide sur cet exercice sur les triangles. J'ai cherché pendant quelques heures déjà et je ne trouve toujours pas :hein:
Le triangle ABC est tel que AC = 13 ; AB = 14 et BC = 15. Soient H, J, K les pieds des hauteurs respectivement des sommets C, A, B.
Montrer que CH est un nombre entier. Montrer que AJ est un nombre décimal. Montrer que BK est un quotient d'entiers. Proposer ensuite un triangle dont les trois côtés et les trois hauteurs aient pour longueur des nombres entiers.
Quelqu'un pour m'aiguiller ici s'il vous plaît ? :hum: Merci beaucoup :we:

par **chombier** » 26 Fév 2015, 21:53

TooLate a écrit:Bonjour à tous.
J'aurais besoin d'aide sur cet exercice sur les triangles. J'ai cherché pendant quelques heures déjà et je ne trouve toujours pas :hein:
Le triangle ABC est tel que AC = 13 ; AB = 14 et BC = 15. Soient H, J, K les pieds des hauteurs respectivement des sommets C, A, B.
Montrer que CH est un nombre entier. Montrer que AJ est un nombre décimal. Montrer que BK est un quotient d'entiers. Proposer ensuite un triangle dont les trois côtés et les trois hauteurs aient pour longueur des nombres entiers.
Quelqu'un pour m'aiguiller ici s'il vous plaît ? :hum: Merci beaucoup :we:

Pour calculer la longueur de CH, le plus simple que je vois est d'abord de calculer la surface du triangles ABC à partir de ses trois longueurs (13, 14 et 15).

Regarde dans ton cours, il doit y avoir une formule pour calculer la surface d'un triangles à partir des longueurs des trois côtés. Si ce n'est pas le cas, c'est sans doute que tu dois utiliser une autre méthode.

par **mathelot** » 26 Fév 2015, 21:53

bonjour,

le triangle ABC est parfaitement déterminé, défini par les mesures de longueurs des côtés.
Tout du triangle (longueurs de médianes, de hauteurs,de bissectrices, de symédianes, mesures des angles,coordonnées des points remarquables,rayons des cercles) peut être calculé.
On dit que le triangle est "résoluble".

Qu'est ce que tu calculerais de prime abord ?

réponse: je suis d'accord avec Chombier, calculer d'abord la mesure d'aire du triangle.

rubrique géométrie: "métrique du triangle"

par **TooLate** » 27 Fév 2015, 21:17

Merci beaucoup pour votre aide à tous sur cette question ! J'ai grâce à vous (et au Héron) résolu la question 1 et la 2 :we:
Cependant, à propos de la dernière question (proposer un triangle dont les 3 côtés et les 3 hauteurs aient pour longueurs des nombres entiers), je ne trouve pas :mur: Un triangle plat ferait-il l'affaire, ou attend-on plus de moi ? :help:
Merci encore ! :we:

par **mathelot** » 27 Fév 2015, 22:35

on multiplie les longueurs par k pour chasser les dénominateurs

par **TooLate** » 28 Fév 2015, 11:00

mathelot a écrit:on multiplie les longueurs par k pour chasser les dénominateurs

Peux-tu être un peu plus précis s'il te plaît ? Je n'ai pas compris :hein:

par **mathelot** » 28 Fév 2015, 11:12

je trouve comme longueurs des hauteurs: 56/5 et 168/13.
on multiplie les mesures de longueurs des côtés par

par **TooLate** » 28 Fév 2015, 13:27

mathelot a écrit:je trouve comme longueurs des hauteurs: 56/5 et 168/13.
on multiplie les mesures de longueurs des côtés par

Peux-tu m'aider sur la démarche sans forcément me donner la réponse s'il te plaît ? :lol3:

par **mathelot** » 28 Fév 2015, 13:33

TooLate a écrit:Peux-tu m'aider sur la démarche sans forcément me donner la réponse s'il te plaît ? :lol3:

calcule l'aire avec la formule de Héron
puis de nouveau la formule d'aire avec une hauteur et une base

ici

par **TooLate** » 28 Fév 2015, 17:26

mathelot a écrit:calcule l'aire avec la formule de Héron

Je veux bien, mais l'aire de quoi ? Je cherche un triangle, on ne me le donne pas :triste:

par **mathelot** » 28 Fév 2015, 17:34

ah d'accord. L'aire est la mesure de la surface délimitée par les trois côtés du triangle.
Le triangle est donné à un déplacement près (translation, rotation)
l'aire est exprimée en unité d'aire qui est l'aire du parallèlogramme unité construit avec
le repère (O,I,J)

par **TooLate** » 28 Fév 2015, 18:28

J'ai un peu de mal à te comprendre :doh:
En quoi cela me permet de trouver un triangle dont les hauteurs et les côtés aient tous des longueurs entières ?

par **mathelot** » 28 Fév 2015, 19:04

TooLate a écrit:J'ai un peu de mal à te comprendre :doh: ?

ce n'est pas moi qu'il faut comprendre mais l'énoncé de l'exercice.
ça fait deux jours qu'on t'a demandé un calcul d'aire de ce triangle.

chombier le 26/02 a écrit:Pour calculer la longueur de CH, le plus simple que je vois est d'abord de calculer la surface du triangles ABC à partir de ses trois longueurs (13, 14 et 15).

peux tu écrire (publier) les résultats que tu as obtenus ? as tu calculé les mesures des hauteurs,
c'est ça qui est demandé ?

par **TooLate** » 28 Fév 2015, 20:04

Oups pardon, j'ai obtenu les résultats suivants :
L'aire du triangle est de 84
La hauteur CH = 12
La hauteur AJ = 11.2
La hauteur BK = 168/13
Maintenant je dois trouver un triangle dont tous les côtés et toutes les hauteurs ont pour longueurs des entiers naturels.

par **mathelot** » 28 Fév 2015, 20:34

je te remercie d'avoir publié tes résultats, ça recentre la conversation. :we:

il y a un procédé de similitude (agrandissement/réduction), par exemple pour les cartes géographiques au 100 000ième , qui consiste à multiplier toutes les distances par un facteur k.

Comme les mesures des hauteurs comportent les dénominateurs 5 et 13, on multiplie les longueurs des côtés de ABC par

, ce qui a pour effet de multiplier toutes les mesures des segments par k et toutes les aires par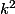

.

les mesures des hauteurs deviennent entières, du coup. Par contre les angles sont inchangés,
leurs sinus sont conservés tels quels dans l'agrandissement.

par **TooLate** » 28 Fév 2015, 21:15

Je te remercie énormément pour toutes ces réponses et pour ta patience, ce qui m'a permi de trouver le résultat :we:
Je n'aurai jamais trouvé ça tout seul !
Finalement, on obtient un triangle avec des dimensions plutôt énormes (je te donne le résultat que j'ai calculé grâce à ta méthode en passant) :
côtés = 845 ; 910 ; 975
aire = 354 900
hauteurs = 728 ; 780 ; 840
Merci encore :we:

par **mathelot** » 28 Fév 2015, 21:22

:we: je te remercie également pour tes encouragements.

Triangles

Triangles

Qui est en ligne