Triangles équilatéraux

[Luciedemuyter]

Bonjour j’ai un dm et math en première S et je sais comment faire lexercice mais j’en narrive pas a le faire MDR!
Alors: [AB] est un segment de longueur 10. M est un point de [AB] et on pose AM=x. On construit, du même côté du segment, les points R et S tels que AMR et MBS soient des triangles équilatéraux.
Existe t’il une position de M sur le segment [AB] pour laquelle l’aire du triangle MRS est maximale?
Merci de m’aider car j’ai voulu faire l’ébauche sinus par rapport à la la et que je tea ce mais je n’arrive pas à aboutir à cela!
Merci de m’aider

[pascal16]

Des pistes (tu es sur quelle leçon ?)

Quand M est en A ou B, la surface est nulle.
en des autres points, elle n'est pas nulle.
Si on suppose la fonction qui relie x à la surface de MRS continue, elle atteint forcément un maximum sur[0;10].
Mais je pense que cette réponse ne correspond pas à l'attente du prof.

calculer directement la surface de MRS est possible par une formule en fonction de la la longue des cotés de MRS, mais bizarrement, cette formule utile n'est pas au programme.

Il reste à se rendre compte que si on trace le triangle équilatéral ABN, on a 5 triangles dont 3 ont des surfaces faciles à calculer et le dernier un peu plus compliqué

[Lostounet]

Salut,

Commence par essayer d'exprimer l'aire d'un triangle équilatéral de côté c (en fonction de c).

Utilise pour cela la formule base*hauteur/2
Où la hauteur est calculée avec le théorème de Pythagore en fonction de c.

Ensuite on appliquera cette formule pour exprimer les aires des deux triangles en fonction de x.

[MMu]

Plus haut on a défini le point tel 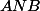équilatéral.
Observe que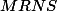 est un paralelogramme donc
.. and so on ..

[aviateur]

Bonjour
Donc il faut faire comme c'est suggéré plus haut. réponds à ces questions:
1. Pour un triangle équilatéral de côté c , quelle est son aire en fonction de c?
2. Utilise cette formule dans celle de l'aire de (MRS) et simplifie l'expression. que trouves-tu?
3. A faire après 1 et 2.

[pascal16]

j'ai fait le tracé avec géogebra.
On dirait bien une parabole et ma réponse est celle à laquelle son s'attend.

[aviateur]

Bonjour
@Pascal16
Sans faire de calcul on peut répondre directement: En effet, c'est clair que que l'aire dépend quadratiquement de x et comme le maximum n'est pas aux extrémités, il ne peut être situé qu'au milieu.
En effet, si ce n'était pas le cas on aurait 2 extremums (à cause de la symétrie du problème) mais ce n'est pas possible pour une fonction quadratique (sauf éventuellement aux extrémités mais on a éliminé cela.)
Donc, tu as dû trouver x=5.