Mais c'est vous qui m'avez dit que c'était H:
"il ne te suffit plus que de montrer que H est le barycentre de A affecté de a² et de H affecté de b²+c²"
Et il faut démontrer que I= bar{(A;a²),(H;a²+c²)}
Triangle rectangle ABC
25 messages
- Page 2 sur 2 - 1, 2
Pour monter que I est le barycentre de (A;a²), (B;b²), (C;c²) il faut montrer que 
Or nous avons montré précédemment que H était le barycentre de (B;b²) et (C;c²) donc il nous suffit de démontrer que I est le barycentre de (A;a²) et (H;b²+c²) ou encore de (A;a²) et (H;a²) puisque a²=b²+c²
Mais c'est le cas puisque I est au milieu de AH, en effet I est bien le barycentre de A et H affecté d'un poids égal. (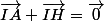 est équivalent à
est équivalent à 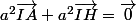
Or nous avons montré précédemment que H était le barycentre de (B;b²) et (C;c²) donc il nous suffit de démontrer que I est le barycentre de (A;a²) et (H;b²+c²) ou encore de (A;a²) et (H;a²) puisque a²=b²+c²
Mais c'est le cas puisque I est au milieu de AH, en effet I est bien le barycentre de A et H affecté d'un poids égal. (
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
