Travaille de pro
25 messages
- Page 2 sur 2 - 1, 2
par Quidam » 21 Oct 2007, 11:54
Je reprends l'explication de farator jusqu'à un certain point.
Tu peux, pour commencer, mettre 2 en facteur :
Donc :
Rappelle-toi certains exercices que tu as faits l'an dernier :
Factoriser x²+2x+1 ! Tiens, c'est une identité remarquable ! Ca fait (x+1)² non ?
Si on te donne : x²-4x+4, tu dois reconnaître l'identité remarquable (a-b)²=a²-2ab+b² et donc voir que x²=x² (he, he !), que 4=2² et que -4x=-2*2*x, d'accord ? Donc x²-4x+4=(x-2)² !
Si on te donne :
, tu dois aussi reconnaître que x²=x², que 
est le carré de 
et que x n'est pas autre chose que le double produit de x par : 
! Donc tu es en présence de la même identité remarquable !
^2 = x^2-2*x*(\frac{1}{2})+(\frac{1}{2})^2=x^2-x+\frac{1}{4})
Ca se corse ! Si à présent on te donne x²+8x ! Que manque-t-il pour faire ton bonheur ? Puisque 8 = 2*4, tu peux écrire x²+8x=x²+2*4*x d'accord ? Alors que manque-t-il pour que cela fasse une identité remarquable ? Eh bien, je pense que tu peux deviner que s'il y avait un "+4²", ça deviendrait x²+8x+4² = x²+2*4*x+4²=(x+4)² !
Par conséquent : x²+8x = x²+8x+4²-4²=(x+4)²-4²
Maintenant, voyons le cas général !
On peut par exemple te proposer de factoriser x²+2x-3 !
Alors, tu peux dire que x²+2x est "le début du développement de (x+1)²" puisque (x+1)²=x²+2x+1. Alors x²+2x=(x+1)²-1 ok ? Et donc, factoriser x²+2x-3, c'est factoriser [(x+1)²-1]-3, soit (x+1)²-4. Mais 4 est le carré de 2 ! Et donc x²+2x+3=(x+1)²-2² et là, tu tombes sur ton identité remarquable préférée : a²-b²=(a+b)*(a-b) ! Par conséquent, x²+2x+3=(x+1)²-2²=[(x+1)+2][(x+1)-2]=(x+3)(x-1) ! Ca y est ! C'est factorisé !
Revenons alors à ton cas particulier :
b²-b est le début du développement de^2)
. En effet, ^2 = b^2-2*b*(\frac{1}{2})+(\frac{1}{2})^2= b^2-b+\frac{1}{4})
Par conséquent,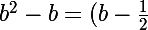^2 - \frac{1}{4})
et par suite :
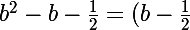^2 - \frac{1}{4}-\frac{1}{2})
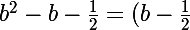^2 - \frac{3}{4})
Mais
est le carré de 
. Donc tu peux écrire :
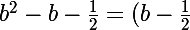^2 - (\frac{\sqrt{3}}{2})^2)
On est en présence à nouveau de la différence de deux carrés : a²-b² qui peut se factoriser : a²-b²=(a+b)*(a-b). Donc,
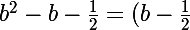^2 - (\frac{\sqrt{3}}{2})^2=[(b-\frac{1}{2})+\frac{\sqrt{3}}{2}][(b-\frac{1}{2})-\frac{\sqrt{3}}{2}])
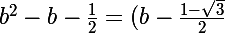(b-\frac{1+\sqrt{3}}{2}))
C'est factorisé !
Par conséquent
est équivalent à :
(b-\frac{1+\sqrt{3}}{2})=0)
Ce qui donne deux solutions :
Tu avais au départ les équations a+b=1 et a²+b²=2 !
Donc a=1-b
à correspond 
et à correspond 
C'est normal ! a et b jouant le même rôle, on peut les échanger !
En résumé, bien que ce soit peut-être un peu difficile pour toi de suivre ce calcul, il se base sur des techniques que tu connais déjà ! Toutes ces histoires de discriminant te seront racontées l'année prochaine : ce que l'on apprend en première, c'est à résoudre ce type d'équation en appliquant des formules toutes faites sans avoir besoin de réfléchir. Ca va plus vite, justement parce que ce n'est pas la peine de réfléchir, mais c'est exactement la même chose que ce que je viens de t'expliquer !
farator a écrit:Bon je t'aide quand même avec les équations du second degré ..
a+b=1 et a²+b²=2
a=1-b et donc (1-b)²+b²=2
Tu développes et tu arrives à :
2b²-2b-1=0
Tu as compris jusqu'ici ?
Tu peux, pour commencer, mettre 2 en facteur :
Donc :
Rappelle-toi certains exercices que tu as faits l'an dernier :
Factoriser x²+2x+1 ! Tiens, c'est une identité remarquable ! Ca fait (x+1)² non ?
Si on te donne : x²-4x+4, tu dois reconnaître l'identité remarquable (a-b)²=a²-2ab+b² et donc voir que x²=x² (he, he !), que 4=2² et que -4x=-2*2*x, d'accord ? Donc x²-4x+4=(x-2)² !
Si on te donne :
Ca se corse ! Si à présent on te donne x²+8x ! Que manque-t-il pour faire ton bonheur ? Puisque 8 = 2*4, tu peux écrire x²+8x=x²+2*4*x d'accord ? Alors que manque-t-il pour que cela fasse une identité remarquable ? Eh bien, je pense que tu peux deviner que s'il y avait un "+4²", ça deviendrait x²+8x+4² = x²+2*4*x+4²=(x+4)² !
Par conséquent : x²+8x = x²+8x+4²-4²=(x+4)²-4²
Maintenant, voyons le cas général !
On peut par exemple te proposer de factoriser x²+2x-3 !
Alors, tu peux dire que x²+2x est "le début du développement de (x+1)²" puisque (x+1)²=x²+2x+1. Alors x²+2x=(x+1)²-1 ok ? Et donc, factoriser x²+2x-3, c'est factoriser [(x+1)²-1]-3, soit (x+1)²-4. Mais 4 est le carré de 2 ! Et donc x²+2x+3=(x+1)²-2² et là, tu tombes sur ton identité remarquable préférée : a²-b²=(a+b)*(a-b) ! Par conséquent, x²+2x+3=(x+1)²-2²=[(x+1)+2][(x+1)-2]=(x+3)(x-1) ! Ca y est ! C'est factorisé !
Revenons alors à ton cas particulier :
b²-b est le début du développement de
Par conséquent,
Mais
On est en présence à nouveau de la différence de deux carrés : a²-b² qui peut se factoriser : a²-b²=(a+b)*(a-b). Donc,
C'est factorisé !
Par conséquent
est équivalent à :
Ce qui donne deux solutions :
Tu avais au départ les équations a+b=1 et a²+b²=2 !
Donc a=1-b
à
et à
C'est normal ! a et b jouant le même rôle, on peut les échanger !
En résumé, bien que ce soit peut-être un peu difficile pour toi de suivre ce calcul, il se base sur des techniques que tu connais déjà ! Toutes ces histoires de discriminant te seront racontées l'année prochaine : ce que l'on apprend en première, c'est à résoudre ce type d'équation en appliquant des formules toutes faites sans avoir besoin de réfléchir. Ca va plus vite, justement parce que ce n'est pas la peine de réfléchir, mais c'est exactement la même chose que ce que je viens de t'expliquer !
par Quidam » 21 Oct 2007, 11:56
Il reste que c'est quand même un peu dur pour toi de "deviner" tout cela tout seul. Et comme il semble, selon certains post ci-dessus, que certain professeurs enseignent cette méthode en seconde, je me demande bien si tu n'es pas dans ce cas-là ! Es-tu certain que ton professeur ne t'a rien expliqué dans ce sens ?
par AL-kashi23 » 21 Oct 2007, 12:42
Bonjour, ca serait quand même plus logique que l'énoncé soit plutôt :
a+b=1
a²-b²=2
étant donné qu'il est en seconde ???
Sinon ....
a+b=1
a²-b²=2
étant donné qu'il est en seconde ???
Sinon ....
par Quidam » 21 Oct 2007, 22:11
AL-kashi23 a écrit:Bonjour, ca serait quand même plus logique que l'énoncé soit plutôt :
a+b=1
a²-b²=2
étant donné qu'il est en seconde ???
Sinon ....
Très juste ! Ca c'est une bonne idée !
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :