Travail sur les indices d'une suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
yaboo
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Avr 2013, 19:15
-
 par yaboo » 01 Fév 2014, 15:02
par yaboo » 01 Fév 2014, 15:02
Bonjour,
Je n'arrive pas à comprendre la méthode pour résoudre le type d'exercice suivant sur les suites :
Soit
)
la suite définie sur

par :
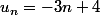
Exprimer

en fonction de

Je sais exprimer

en fonction de

mais pas l'exercice ci-dessus...
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Fév 2014, 15:08
par siger » 01 Fév 2014, 15:08
Bonjour
??????
le terme U(n) veut dire le terme de rang n , donc U(n+1) s'exprime donc de la meme maniere en fonction du rang n+1
U(n) = -3*(n) + 4
U(n+1) = -3*(n+1) + 4 = -3n + 1
-
yaboo
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Avr 2013, 19:15
-
 par yaboo » 01 Fév 2014, 15:16
par yaboo » 01 Fév 2014, 15:16
Merci de la réponse. Mais je ne pense pas que ce soit correct.
Ce que tu viens de faire c'est "exprimer

en fonction de

" et non "en fonction de

"
Il y a le résultat dans mon livre, et nous devrions trouver
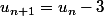
Mais aucune démonstration ou explication n'est faite...
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 01 Fév 2014, 15:23
par Manny06 » 01 Fév 2014, 15:23
yaboo a écrit:Merci de la réponse. Mais je ne pense pas que ce soit correct.
Ce que tu viens de faire c'est "exprimer

en fonction de

" et non "en fonction de

"
Il y a le résultat dans mon livre, et nous devrions trouver
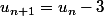
Mais aucune démonstration ou explication n'est faite...
tu dires d'abord n en fonction de Un et tu remplaces dans la formule donnant Un+1 en fonction de n
-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 01 Fév 2014, 15:49
par siger » 01 Fév 2014, 15:49
yaboo a écrit:Merci de la réponse. Mais je ne pense pas que ce soit correct.
Ce que tu viens de faire c'est "exprimer

en fonction de

" et non "en fonction de

"
Il y a le résultat dans mon livre, et nous devrions trouver
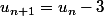
Mais aucune démonstration ou explication n'est faite...
Toutes mes excuses, j'ai lu l'enoncé trop vite!
mais U(n+1) = -3n+1
Un = -3n + 4 d'ou -3n = Un -4
et U(n+1) = Un -4 + 1 = Un -3
-
yaboo
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Avr 2013, 19:15
-
 par yaboo » 01 Fév 2014, 16:01
par yaboo » 01 Fév 2014, 16:01
D'accord ! Merci beaucoup j'ai compris ! C'était tout bête en fait ^^
Par contre, en essayant de faire l'exercice suivant, je re-bloque :s
"Soit
)
la suite définie sur N par
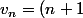^2)
"
Exprimer

en fonction de

J'ai déjà exprimé

en fonction de

ce qui fait :
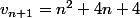
Par contre avec le carré je suis perdu...
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 01 Fév 2014, 16:12
par Manny06 » 01 Fév 2014, 16:12
yaboo a écrit:D'accord ! Merci beaucoup j'ai compris ! C'était tout bête en fait ^^
Par contre, en essayant de faire l'exercice suivant, je re-bloque :s
"Soit
)
la suite définie sur N par
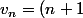^2)
"
Exprimer

en fonction de

J'ai déjà exprimé

en fonction de

ce qui fait :
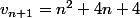
Par contre avec le carré je suis perdu...
Vn+1=(n+1)²+2(n+1)+1 = Vn+2V(Vn)+1 ou bien (V(Vn)+1)²
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
en fonction de
" et non "en fonction de
"
en fonction de
" et non "en fonction de
"
la suite définie sur N par
"
en fonction de
en fonction de
ce qui fait :