Transformation et complexes

[Anonyme]

Bonsoir tout le monde!
J'ai un exercice à faire mais j'y comprend rien du tout pourriez vous m'aider svp
Soit f l'application qui, à tout nombre complexe z différent de i, associe z' tel que :
z'= f(z)=i+(2/(zbare+i))
On note T l'application du plan complexe privé du point A d'affixe i, dans le plan complexe, définie par M' =T(M), M et M' étant les points d'affixes respectives z et z'.
1a) Calculer arg[(z'-i)(zbare+i)]
Que peut on en deduire pour les points A,M et M'?
b)Exprimer l'affixe z" de M" = (T ° T)(M) en fonction de l'affixe de M.Que peut on dire de T°T?
c)On appelle J l'ensemble des points de P invariants par T
Donner une condition portant sur AM pour que le point M d'affixe z appartienne à J
Caracteriser geometriquement J
2)Dans cette question, on suppose que z=1+i+exp(i teta) où teta est un nombre réel; on notera B le point d'affixe 1+i
a)Quelle est la courbe t décrite par le point M, d'affixe z, lorsque teta decrit ]-pi/2;pi/2[ ?
b)Calculer z'-i = f(z)-i en fonction de teta/2
A quelle courbe L appartient le point M' d'affixe z'?
c)En deduire T(t), image par T de t
Merci beaucoup par avance et joyeux noel à tous

[becirj]

Bonjour
Voyons le démarrage.
1. donc
2 est un réel positif, il a pour argument 0 modulo
Un produit a pour argument la somme des arguments des facteurs donc
est le conjugué de 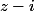, 2 complexes conjugués ont des arguments opposés, on a donc



soit
Les points A, M et M' sont alignés, on peut ajouter que les vecteurs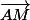 et sont de même sens.