Bonjour,
Je rencontre des problèmes pour tracer la courbe x=(3/y)-y, avec y en ordonnée
J’ai essayé de l’exprimer de facon qu’il n’y ait qu’un seul y, mais je n’y arrive pas... je ne sais pas comment faire après le x=(3-y^2)/y
Merci en avance pour votre aide
Tracer une courbe
8 messages
- Page 1 sur 1
Re: Tracer une courbe
bonjour,
je te propose d'étudier x fonction de y. On pose
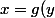:= \dfrac{3-y^2}{y})
calculer g'(y) puis dresser le tableau de variations et les asymptotes. On note que g est une fonction impaire.
je te propose d'étudier x fonction de y. On pose
calculer g'(y) puis dresser le tableau de variations et les asymptotes. On note que g est une fonction impaire.
Re: Tracer une courbe
Continuons sur la piste que tu proposes.
Tu arrives à
Donc , sous certaines conditions,
Et donc
Sinon, tu as une autre piste, un peu inhabituelle. Pour chaque valeur de y, tu as une formule qui te permet de calculer x. Tu peux imaginer : tu tournes la feuille d'un quart de tour, l'axe y est horizontal, l'axe x est vertical. Et tu traces la courbe dans cet environnement.
Puis tu remets ta feuille dans la position initiale.
Tu arrives à
Donc , sous certaines conditions,
Et donc
Sinon, tu as une autre piste, un peu inhabituelle. Pour chaque valeur de y, tu as une formule qui te permet de calculer x. Tu peux imaginer : tu tournes la feuille d'un quart de tour, l'axe y est horizontal, l'axe x est vertical. Et tu traces la courbe dans cet environnement.
Puis tu remets ta feuille dans la position initiale.
Re: Tracer une courbe
lyceen95 a écrit:Sinon, tu as une autre piste, un peu inhabituelle. Pour chaque valeur de y, tu as une formule qui te permet de calculer x. Tu peux imaginer : tu tournes la feuille d'un quart de tour, l'axe y est horizontal, l'axe x est vertical. Et tu traces la courbe dans cet environnement.
Puis tu remets ta feuille dans la position initiale.
il faut faire attention que l'axe des y, après rotation d'un quart de tour, est orienté "les y croissant vers la gauche"
Re: Tracer une courbe
Il faut supposer que deux mathématicien(ne)s étudient la fonction g (et sa courbe).
Le 1er est un analyste: il calcule la dérivée (variable y) , détermine les limites aux bornes du domaine de définition (variable y) , dresse le tableau des variations de g, étudie les asymptotes. Il détermine le signe des "quantités" , décrit les variations de g, calcule la position de la courbe de g par rapport à ses asymptotes.
Ensuite, entre en scène le géomètre. Dans le repère du plan habituel, en s'appuyant sur les résultats de l'analyste, il place les points de la courbe de g dans les quatre quadrants du plan, en ayant déterminé les deux asymptotes de la courbe de g.
travail de l'analyste:
soit=\dfrac{3-y^2}{y})
=...)
 = ...)
 = ...)
montrer que g est impaire. la courbe de g est symétrique par rapport à ...
La droite (D) d'équation x=....... est asymptote à la courbe de g. La courbe est située au dessus/dessous de son asymptote (D)
Le 1er est un analyste: il calcule la dérivée (variable y) , détermine les limites aux bornes du domaine de définition (variable y) , dresse le tableau des variations de g, étudie les asymptotes. Il détermine le signe des "quantités" , décrit les variations de g, calcule la position de la courbe de g par rapport à ses asymptotes.
Ensuite, entre en scène le géomètre. Dans le repère du plan habituel, en s'appuyant sur les résultats de l'analyste, il place les points de la courbe de g dans les quatre quadrants du plan, en ayant déterminé les deux asymptotes de la courbe de g.
travail de l'analyste:
soit
montrer que g est impaire. la courbe de g est symétrique par rapport à ...
La droite (D) d'équation x=....... est asymptote à la courbe de g. La courbe est située au dessus/dessous de son asymptote (D)
Re: Tracer une courbe
Bonjour,
variable y et x fonction de y:
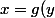=-y+\dfrac{3}{y})
domaine de définition de g: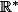
dérivée de g:
=-1-\dfrac{3}{y^2})
d'où<0)
g est décroissante sur
g est impaire. La courbe de g est symétrique par rapport à l'origine O du repère.
On garde le repère habituel orthonormé direct (axe des x horizontal et croissant vers la droite)
Limites aux bornes du domaine et droites asymptotes à la courbe de g:
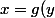=-y+\dfrac{3}{y})
Les points) et
et )
=- \infty) . la courbe de g admet pour asymptote la
. la courbe de g admet pour asymptote la
droite d'équation x=-y. La courbe de g est au dessus de son asymptote x=-y
C'est ce qu'il se passe dans le deuxième quadrant du plan
=+ \infty) La courbe de g admet pour asymptote l'axe des x.
La courbe de g admet pour asymptote l'axe des x.
Et la courbe de g est au dessus de l'axe des x. C'est ce qu'il se passe dans le premier quadrant du plan
On complète la courbe de g par symétrie par rapport à l'origine O.
variable y et x fonction de y:
domaine de définition de g:
dérivée de g:
d'où
g est décroissante sur
g est impaire. La courbe de g est symétrique par rapport à l'origine O du repère.
On garde le repère habituel orthonormé direct (axe des x horizontal et croissant vers la droite)
Limites aux bornes du domaine et droites asymptotes à la courbe de g:
Les points
droite d'équation x=-y. La courbe de g est au dessus de son asymptote x=-y
C'est ce qu'il se passe dans le deuxième quadrant du plan
Et la courbe de g est au dessus de l'axe des x. C'est ce qu'il se passe dans le premier quadrant du plan
On complète la courbe de g par symétrie par rapport à l'origine O.
Re: Tracer une courbe
sinon, on a les équivalences:




on obtient la réunion de deux courbes d'équations


on obtient la réunion de deux courbes d'équations
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
