Toujours ces limites...

par **MarionDD** » 01 Nov 2010, 17:49

j'ai deux limites d'une même fonction à trouver, j'en ai trouvé une mais impossible de trouver l'autre. je suis sure que c'est tout bête mais j'ai pas le déclique..

pour celle là, j'ai sans problème utilisé le théorème de comparaison :

on a donc

avec

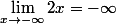
donc par comparaison

maintenant je trouver

Et là ça coince, je ne peux pas réutiliser l'encadrement précédent, la fonction n'est pas paire,.. je ne vois pas trop comment faire.

quelqu'un pourrait m'aider?

merci.

par **GuillaumeRR** » 01 Nov 2010, 17:57

Moi je sais pas...toi qui étais contre les aides car tu n'aura pas de forum au bac...hahahaha

par **MarionDD** » 01 Nov 2010, 17:58

c'est vrai mais au moins ça me fait chercher ^

par **Arnaud-29-31** » 01 Nov 2010, 18:04

Tu as essayé de factoriser l'expression par x² ?

par **Arnaud-29-31** » 01 Nov 2010, 18:12

Attention, lorsque tu passes de

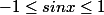
à

, ton x est positif ou négatif ?

par **MarionDD** » 01 Nov 2010, 18:37

j'avance pas même en factorisant par

j'obtiens donc

par **Arnaud-29-31** » 01 Nov 2010, 18:38

Oui ... il y'a un petit carré en trop, mais on a fait apparaître qqch qui tend vers 0.

par **MarionDD** » 01 Nov 2010, 18:42

oui pardon c'est 2/x.

quand on encadre 2/x - (sinx)^2 on a 2/x à gauche et 2/x - 1 à droite

alors 2/x tend vers 0+ et 2/X - 1 tend vers -1 (quand x tend vers + l'infini)

mais je vois pas comment on peut conclure :s

par **Arnaud-29-31** » 01 Nov 2010, 18:58

Et si par exemple tu regarde l'expression de

et celle de

avec k entier relatif. Ca donne quoi ?

par **MarionDD** » 01 Nov 2010, 19:05

euh euh euh... la je commence à plus être opérationnelle ^^

ça m'énerve! je vois pas du tout avec f(k.pi) et f(k.pi/2)

par **Arnaud-29-31** » 01 Nov 2010, 19:12

Bon ... As tu compris qu'il allait être trèèèès dur de trouver une limite en

?

par **MarionDD** » 01 Nov 2010, 19:19

ah ben oui parce que c'est déjà très dur d'en trouver une...je n'arrive même pas à la visualiser sur la calculatrice. ça veut dire qu'elle n'existe pas ?

par **Arnaud-29-31** » 01 Nov 2010, 19:20

Oui, il n'y a pas de limite. Et on peut par exemple le montrer en étudiant l'expression de

et celle de

par **GuillaumeRR** » 01 Nov 2010, 19:21

tout ça pour ça???! ^^' :hum:

par **MarionDD** » 01 Nov 2010, 19:28

Pas de limite...ça c'est du nouveau pour moi.

on l'explique en montrant que c'est périodique alors ? pourquoi en utilisant ces expressions et pas la fonction directement ?

par **Arnaud-29-31** » 01 Nov 2010, 19:34

Ce n'est pas périodique non plus ...

Tu es d'accord que si une fonction f telle que f(x) tend vers une certaine limite (incluant l'infini) en

, alors f(qqch) tend vers cette limite si le qqch tend vers l'infini ??
Je sais pas si c'est clair dis comme ca ... :s

par **MarionDD** » 01 Nov 2010, 19:36

je suis vraiment désolée mais je comprends pas du tout. :/

par **Arnaud-29-31** » 01 Nov 2010, 19:39

Et bien si f admetait une limite en

alors

et

tendraient vers cette limite quand k tend vers

... or

et

ne tendent pas vers la même chose.

par **MarionDD** » 01 Nov 2010, 19:41

donc f n'admet pas de limite en +l'infini. donc dans mon cas, je peux prendre quelles valeurs pour montrer que ma fonction n'admet pas de limites en + l'infini

par **Arnaud-29-31** » 01 Nov 2010, 19:49

Et bien comme je t'ai dis regarde ce que donnent

et

... c'est pas très difficile.

Toujours ces limites...

toujours ces limites...

Qui est en ligne