[Petit défi 2nde - 1re - Tle (sections confondues)]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 01 Nov 2009, 02:58
par Dinozzo13 » 01 Nov 2009, 02:58
Bonjour, comme je suis de bonne humeur aujourd'hui, je propose mon premier défi. Comme dit dans le titre, ce défi s'adresse surtout à des élèves de 2nde, 1re voire de Tle toutes sections confondues, car je suppose qu'il s'agit d'un jeux d'enfant pour les post-bac :ptdr: :
Soient

,

et

trois réels tels que
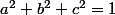
:
1°) Calculer
^2+(ac-b)^2)
.
2°) Calculer
)
, aide : penser à
^2)
.
3°) En déduire
^2+(ac-b)^2}{1-2(ab+bc+ac)})
.
Amusez-vous bien :we:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 01 Nov 2009, 10:31
par benekire2 » 01 Nov 2009, 10:31
Dinozzo13 a écrit:Bonjour, comme je suis de bonne humeur aujourd'hui, je propose mon premier défi. Comme dit dans le titre, ce défi s'adresse surtout à des élèves de 2nde, 1re voire de Tle toutes sections confondues, car je suppose qu'il s'agit d'un jeux d'enfant pour les post-bac :ptdr: :
Soient

,

et

trois réels tels que

:
1°) Calculer

.
2°) Calculer

, aide : penser à

.
3°) En déduire

.
Amusez-vous bien :we:
Oui en effet c'est un jeu d'enfant dès la première S je pense, en fait tu guide trop ...
Par contre pour la filière L ou la seconde, il s'avère un très bon entraînement.
Je propose un exercice niveau seconde dans la foulée!!
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 10:33
par Timothé Lefebvre » 01 Nov 2009, 10:33
Yop,
en fait tu peux passer de l'énoncé à la dernière question directos (enfin pour les motivés quoi).
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 01 Nov 2009, 12:32
par Dinozzo13 » 01 Nov 2009, 12:32
Le pblm c'est que si je ne guide pas un peu, ça devient moins évident :triste: .
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 01 Nov 2009, 15:00
par benekire2 » 01 Nov 2009, 15:00
Ouais mais bon, c'est quand même légèrement trop guidé... Sinon tu guide petit à petit!!
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 01 Nov 2009, 15:03
par benekire2 » 01 Nov 2009, 15:03
Enorme ^^ Enfin toujours est-il que l'on se base sur notre jugement, qui, c'est sûr ne sera pas le même que celui de ceux qui ne sont pas a fond dans les maths.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 15:04
par Timothé Lefebvre » 01 Nov 2009, 15:04
Tout à fait d'accord, et cet exo était destiné à tous les lycéens.
Bref, je re je vais goûter :lol2:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 01 Nov 2009, 15:10
par benekire2 » 01 Nov 2009, 15:10
Timothé Lefebvre a écrit:Tout à fait d'accord, et cet exo était destiné à tous les lycéens.
Bref, je re je vais goûter :lol2:
Glouton, arrête un peu de manger !!
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 16:59
par axel031 » 01 Nov 2009, 16:59
Dinozzo13 a écrit:Bonjour, comme je suis de bonne humeur aujourd'hui, je propose mon premier défi. Comme dit dans le titre, ce défi s'adresse surtout à des élèves de 2nde, 1re voire de Tle toutes sections confondues, car je suppose qu'il s'agit d'un jeux d'enfant pour les post-bac :ptdr: :
Soient

,

et

trois réels tels que
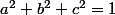
:
1°) Calculer
^2+(ac-b)^2)
.
2°) Calculer
)
, aide : penser à
^2)
.
3°) En déduire
^2+(ac-b)^2}{1-2(ab+bc+ac)})
.
Amusez-vous bien :we:
Comment tu trouves la 2) ??
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 17:03
par Timothé Lefebvre » 01 Nov 2009, 17:03
benekire2 a écrit:Glouton, arrête un peu de manger !!
Moi ?? Tu dois te tromper de personne :lol2:
@ axel31 : développe (a+b+c)² pour voir ?
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 17:05
par axel031 » 01 Nov 2009, 17:05
bah a² + b² + c² + 2ab + 2bc + 2ca ...
mais la c 'est -2(ab+bc+ca)
-
axel031
- Membre Naturel
- Messages: 13
- Enregistré le: 01 Nov 2009, 11:49
-
 par axel031 » 01 Nov 2009, 17:08
par axel031 » 01 Nov 2009, 17:08
bah je crois pas qu il y est une identité remarquable comme celle ci ( c est a dire a² + b² + c² - 2ab - 2bc - 2ca ...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 17:13
par Timothé Lefebvre » 01 Nov 2009, 17:13
On a, d'après l'énoncé, a²+b²+c²=1 :id:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 01 Nov 2009, 17:36
par benekire2 » 01 Nov 2009, 17:36
Et après facto par 2...
Ok je sors
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 01 Nov 2009, 17:40
par Timothé Lefebvre » 01 Nov 2009, 17:40
Ah, heureusement que tu le précises, je n'avais pas vu :ptdr:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 01 Nov 2009, 19:08
par Dinozzo13 » 01 Nov 2009, 19:08
Je vous donne la correction ^^ :
1°) Ici il faut développer, puis factoriser pour faire apparaître
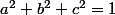
:
^2+(ac-b)^2)
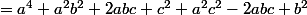
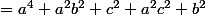
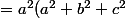+b^2+c^2)
Or
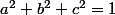
donc
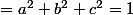
2°) Ici, on sait (ou on calcule) que :
^2=a^2+b^2+c^2+2ab+2bc+2ac)
donc
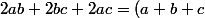^2-(a^2+b^2+c^2))
Par conséquent
=1^2-1=0)
et donc
=1-0=1)
3°) D'après 1°) et 2°) :
^2+(ac-b)^}{1-2(ab+bc+ac)}=\frac{1}{1}=1)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
,
et
trois réels tels que
:
.
, aide : penser à
.
.
,
et
trois réels tels que
:
.
, aide : penser à
.
.