Ln

[tilmo]

bonsoir!
on a n un entier naturel tel que n3
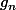
on considere la fonction definie sur tel que:
gn(x)=nx+2ln(x)
1-poser le tableau de variations de gn
2-montrer que ()
3-montrer que l'equation gn(x)=0 admet une seule solution an dans et que
4-deduire la lim de an en +linf
je vous demande de m'aider et merci d'avance!

[farator]

Tiens un schizophrène :)
Tu te souhaites bon travail à toi-même ?! ;)

Tu sais calculer une dérivée .. ?

[Timothé Lefebvre]

Bonsoir tilmo.

Je te prie de bien vouloir modifier ton message, comme te le fait remarquer farator, ce n'est pas à nous de faire ton devoir mais bien à toi.

[tilmo]

voila!mon probleme ne concerne pas la première question j'ai juste ecri l'enoncé!j'ai besoin d'aide pour les autres questions!

[maturin]

pour la 2 tu peux déjà commencer par faire un changement de variable en posant x=y² (tu as le droit car x>0)

ensuite étudie le signe de y-2ln(y) en faisant dérivée étude du signe de la dérivée, déduction du la croissance/décroissance et des maximum et minimum
(ici il faut montrer que le minimum est > 0)

Tu peux faire la même chose sans changement de variable, c'est des calculs plus chiants mais ça marche aussi.


pour la 3 c'est le même genre, regarde si ta fonction est croissante ou non, regarde la valeur en x=0+ et en +inf, déduis la réponse. Regarde en x=1/n et x=1/rac(n), déduis l'encadrement.

[Florélianne]

[font=Arial Black][font=Arial]Bonjour,
on a n un entier naturel tel que n[img]images/latex/2d9362c6490cded6ecd93e0bf42a25bb.gif[/img]3
on considere la fonction [img]images/latex/4114c7d8a6c5b8facb1b81a0f35a213d.gif[/img] definie sur [img]images/latex/d4f6d383a554c82c2c22d70e951a4f43.gif[/img][/font][/font][font=Arial Black][font=Arial]tel que:[/font][/font]
[font=Arial Black][font=Arial] gn(x)=nx+2ln(x)
1. poser le tableau de variations de gn
2. montrer que ([img]images/latex/86de11c9cd033b530a37f36f44b9119d.gif[/img]) [img]images/latex/06274558e2ad5b3c01530e9c5f615ac8.gif[/img] [/font][font=Arial]tu peux étudier h(x) = Vx - lnx sur IR+*
calculer h' et en déduire que h(x) > 0 sur IR+*
[/font][font=Arial][size=2][/font][font=Arial]
[/font] [font=Arial]3. montrer que l'équation gn(x)=0 admet une seule solution an dans [img]images/latex/d4f6d383a554c82c2c22d70e951a4f43.gif[/img] et que [img]images/latex/6f99d0ec575ae84f8d893c5d97386e2d.gif[/img]
[/font][font=Arial]tu as du trouver que gn est croissante de -infini à +infini
gn est une fonction dérivable donc [/font][/size][/font][font=Arial Black][font=Arial][size=2]continue.[/font][/size][/font][font=Arial Black][font=Arial][size=2] Toute fonction continue ne peut changer de signe sans s'annuler
donc ...
comme gn est strictement croissante la solution est unique

reste à justifier l'encadrement...
calcule les deux quantités indiqués et en utilisant la question 2) conclue
[/font][font=Arial]
4. deduire la lim de an en +inf[/font]
[font=Arial]utilise l'encadrement précédent, et cherche les limites de chacune des deux suites pour trouver celle de an

Bon travail
[/font][/size][/font]