Bonjour a tous
J'espere que tout va pour le mieux dans vos vies respectives
Alors je vous prensente mon probleme et bien enfaite j'aimerai
Seulement savoir ce que signifie le "d" dans la notation dx ou df
On l'aborde en mecanique et en math de maniere intuitive sans jamais
Preciser son origine et ce que veut dire , si quelqu'un en saurait un peu
Plus ...
Merci de votre attention
Dx , dt , df ?
5 messages
- Page 1 sur 1
Revois un cours pour les dérivées et les différentielles et après reviens avec les vraies interrogations ? ...
Salut !
le " " représente un élément infinitésimal élémentaire (très très petit).
" représente un élément infinitésimal élémentaire (très très petit).
Exemple : Si tu as un rectangle de longueur et de largeur
et de largeur  , alors un petit élément de longueur est
, alors un petit élément de longueur est 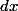 et un petit élément de largeur est
et un petit élément de largeur est 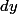 .
.
Remarque : Ainsi un petit élément de surface de ce rectangle est :+++:
:+++:
le "
Exemple : Si tu as un rectangle de longueur
Remarque : Ainsi un petit élément de surface de ce rectangle est
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
le "" représente un élément infinitésimal élémentaire (très très petit).
Exemple : Si tu as un rectangle de longueuret de largeur
, alors un petit élément de longueur est
et un petit élément de largeur est
.
Remarque : Ainsi un petit élément de surface de ce rectangle est:+++:
dx, df, dy, etc. on appelle ça des différentielles.
Le rôle d'une différentielle est plutôt ambigû... On l'utilise en maths comme une pure notation, en tant qu'infiniment petit pour un accroissement d'une fonction selon toutes ses variables. Mais en physique on lui préfèrera la signification d'élément très petit (on ne sait pas a priori à quel point) d'une grandeur d'état (d'un système) ou d'une fonction donnée.
Le but d'une différentielle est de pouvoir jongler entre le rôle d'un accroissement et la dérivée de la fonction correspondante et en général faire des primitivations rapides en regardant la dérivation comme étant le rapport de deux différentielles.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
