X, y et z
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hafsa71
- Membre Naturel
- Messages: 47
- Enregistré le: 02 Nov 2012, 20:42
-
 par hafsa71 » 22 Déc 2012, 21:15
par hafsa71 » 22 Déc 2012, 21:15
bonsoir à tous
soit x ,y et z des réels positifs tel que : x+y+z=1
montrez que :
+sqrt(4y+1)+sqrt(4z+1)<=5)
Besoin de votre aide si possible

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 22 Déc 2012, 23:24
par Ericovitchi » 22 Déc 2012, 23:24
Ça fait la cinquième fois que tu postes une inégalité style olympiade. tu ne réagis à aucun post. Tu fais ça dans quel cadre exactement ? tu as compris les exercices précédents au moins ? Ce sont tous des exercices assez difficiles à trouver dans un cadre estudiantin normal, alors ? tu veux vraiment une solution, et pourquoi ?
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 23 Déc 2012, 01:24
par adrien69 » 23 Déc 2012, 01:24
J'ai trois méthodes.
Une que tu ne comprendrais probablement pas à cause des outils qu'elle utilise et qui ne marche de toute façon que si j'affaiblis l'énoncé (même si je la soupçonne de pouvoir induire le résultat), je dis toujours ça pourrait intéresser quelqu'un : il s'agit d'un développement en série entière que je ne peux faire que si x,y et z sont <1/4
Une que tu comprendrais avec un tout petit peu de hors programme (ou un coup d'oeil à wikipedia), qui fonctionne mais que je n'aime pas parce quelle pue l'astuce à plein nez. Mais en tout cas ça veut dire que ton truc est faisable avec des méthodes élémentaires. Donc tu peux chercher tu devrais finir par trouver.
Une que j'aime beaucoup et qui marche mais que là tu ne comprendrais pas du tout non plus. J'en donne quand même l'idée : voir l'expression dans l'inégalité comme une fonction de deux variables.
-
hafsa71
- Membre Naturel
- Messages: 47
- Enregistré le: 02 Nov 2012, 20:42
-
 par hafsa71 » 23 Déc 2012, 01:47
par hafsa71 » 23 Déc 2012, 01:47
pour éclaircir les choses , je ne me prépare pas pour des olympiades et au fait il ne s'agit que d'un DM que je suis censée résoudre c'est tout quoique le degré de difficulté soit un peu élevé .certes oui ,j'aimerais bien que vous m'aidiez ,en ce qui concerne les autres posts , je les ai plus ou moins compris c'est vrai que j'ai trouvé pas mal de difficultés pour les décrypter mais bon sinon merci pour votre aide

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Déc 2012, 18:29
par Ericovitchi » 23 Déc 2012, 18:29
Pose a=4x+1;b=4y+1;c=4z+1
on a donc a+b+c=4(x+y+z)+3=7 et on doit montrer que

Il faut connaître l'inégalité de Cauchy-Schwarz : Si a1,a2,...an,b1,b2,...bn sont des réels alors
(a1²+..+an²)(b1²+...+bn)²;)(a1b1+..+anbn)²
(géométriquement c'est l'écriture que
^2)
qui est évident puisque (
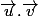^2=|\vec{u}|^2|\vec{v}|^2cos^2)
)
)
Si on prend la suite b1 à b3 = 1 et

;

;

ça donne :
^2\le(a+b+c)(1+1+1)=21)
donc

-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 23 Déc 2012, 19:24
par adrien69 » 23 Déc 2012, 19:24
Ericovitchi a écrit:Pose a=4x+1;b=4y+1;c=4z+1
on a donc a+b+c=4(x+y+z)+3=7 et on doit montrer que

Il faut connaître l'inégalité de Cauchy-Schwarz : Si a1,a2,...an,b1,b2,...bn sont des réels alors
(a1²+..+an²)(b1²+...+bn)²;)(a1b1+..+anbn)²
(géométriquement c'est l'écriture que
^2)
qui est évident puisque (
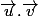^2=|\vec{u}|^2|\vec{v}|^2cos^2)
)
)
Si on prend la suite b1 à b3 = 1 et

;

;

ça donne :
^2\le(a+b+c)(1+1+1)=21)
donc

Une autre méthode : on remarque que

est concave.
On pense donc à l'inégalité de Jensen, qu'il faut connaître (je ne sais pas ce qui est le plus simple conceptuellement, Jensen ou Cauchy-Schwarz, auquel je n'avais pas pensé, bien ouéj Ericovitchi)
On pose alors a=b=c=1/3
a+b+c=1
Donc on a
+1}=\sqrt{7/3})
On a donc

CQFD
Autre méthode basée sur l'analyse à plusieurs variables :
on pose z=1-x-y
et on étudie la fonction de deux variables
=\sqrt{4x+1}+\sqrt{4y+1}+\sqrt{4(1-x-y)+1})
mais là je sors loin du cadre du programme du lycée.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 23 Déc 2012, 19:41
par Ericovitchi » 23 Déc 2012, 19:41
Oui c'est vrai c'est plutôt plus naturel avec l'inégalité de Jensen finalement.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
qui est évident puisque (
)
;
;
ça donne :
donc