J'ai un DM à faire pendant les vacances, et je m'en sors pas trop =s
Un peu d'aide ça serait sympa... J'ai reussi à faire la question 1, et le petit A de la 2...
Et la je bloque bloque bloque :s
L'énoncé:
OIJ et OKL sont deux triangles rectangles isocèles tels que (OI,OJ) = +pi/2 et (OK,OL) = + pi/2
OIML est un parallélogramme.
On se propose de démontrer que :
IK = JL, OM = JK, (IK) 1 (JL) et (OM) 1 (JK).
1. Avec le produit scalaire
a) Démontrer que (OJ,OK) + (OL,OI) = +pi
Exprimer cos (OL, Ol ) en fonction de cos (OJ, OK ).
b) Démontrer que IK = JL et IK JL = 0 en utilisant le
fait que IK = OK - OI et JL = ÔL - OJ.(en terme de vecteur)
c) De façon analogue, démontrer que OM = JK et OM JK = 0.
2. Avec les coordonnées
On munit le plan du repère orthonormal (o ; Ol, OJ ) et on note (a; b) les coordonnées du point K dans ce repère.
a) Quelles sont les coordonnées des points I et J ?
=> A partir d'ici j'y arrive pas...
b) Démontrer que les coordonnées de L sont (- b ; a).
En déduire les coordonnées de M.
c) Calculer les coordonnées des vecteurs IK, JL, OM et JK.
d) Conclure.
La figure:
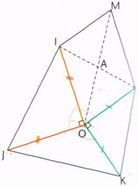
ps: si vous avez besoin de plus d'infos n'hésitez pas... =D
Merci par avance =D
